
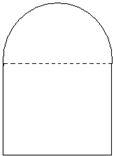
 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 4+π |
| 2 |
| p |
| π+4 |
| p2 |
| 2π+8 |
| p |
| π+4 |
| p |
| π+4 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
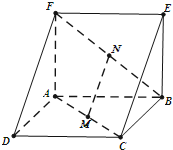 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| cosB |
| cosC |
| b |
| 2a+c |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+1 |
| x-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m+n+l |
| x+y+z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com