
设 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若角 ,
, 边上的中线
边上的中线 的长为
的长为 ,求
,求 的面积.
的面积.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分) 的三个内角
的三个内角 所对的边分别为
所对的边分别为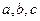 ,向量
,向量 ,
, ,且
,且 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)现在给出下列三个条件:① ;②
;② ;③
;③ ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定 ,求出所确定的
,求出所确定的 的面积.
的面积.
(注:只需要选择一种方案答题,如果用多种方案答题,则按第一方案给分).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图2,渔船甲位于岛屿 的南偏西
的南偏西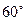 方向的
方向的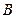 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从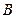 处出发沿北偏东
处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求 的值.
的值.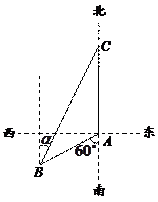
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
、已知向量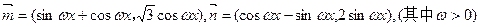 ,
,
函数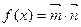 ,若
,若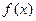 相邻两对称轴间的距离为
相邻两对称轴间的距离为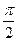 。
。
(1)求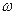 的值
的值 ,并求
,并求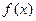 的最大值及相应x的集合;
的最大值及相应x的集合;
(2)在△ABC中,a,b,c分别是A,B,C所对的边,△AB C的面积
C的面积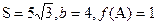 ,求边a的长。
,求边a的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com