
如图,在梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=a,AD=3a,且∠ADC=arcsin
,AB=a,AD=3a,且∠ADC=arcsin![]() ,又PA⊥平面ABCD,AP=a.
,又PA⊥平面ABCD,AP=a.
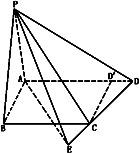
求:(1)二面角P-CD-A的大小(用反三角函数表示);
(2)点A到平面PBC的距离.
|
解析:(1)作C ∵∠ADC=arcsin ∴sin∠CD ∴CD= ∵AD=3a,∴A 又在RtΔABC中,AC= ∵PA⊥平面ABCD,∴PA⊥AC,PA⊥AD,PA⊥AB. 在RtΔPAB中,可得PB= 在RtΔPAC中,可得PC= 在RtΔPAD中,PD= ∵PC2+CD2=( ∴cos∠PCD<0,则∠PCD>90° ∴作PE⊥CD于E,E在DC延长线上,连AE,由三垂线定理的逆定理得AE⊥CD,∠AEP为二面角P-CD-A的平面角. 在RtΔAED中∠ADE=arcsin ∴AE=AD·sin∠ADE=3a· 在RtΔPAE中,tan∠PEA= ∴∠AEP=arctan (2)∵AD⊥PA,AD⊥AB,∴AD⊥平面PAB. ∵BC∥AD,∴BC⊥平面PAB. ∴平面PBC⊥平面PAB,作AH⊥PB于H,∴AH⊥平面PBC. AH为点A到平面PBC的距离. 在RtΔPAB中,AH= 即A到平面PBC的距离为 说明:(1)中辅助线AE的具体位置可以不确定在DC延长线上,而直接作AE⊥CD于E,得PE⊥CD,从而∠PEA为所求,同样可得结果,避免过多的推算.(2)中距离的计算,在学习几何体之后可用“等体积法”求. |


科目:高中数学 来源: 题型:
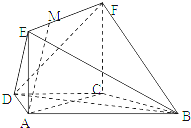 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:
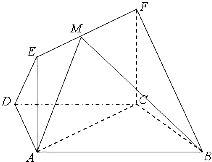 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com