对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时
①求f0(x)和fk(x)的解析式;
②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
解:(1)①f
0(x)=Φ(x))=2
x,x∈(0,2];f
k(x)=Φ(x-2k)+3k=2
x-2k+3k,x∈(2k,2k+2],k∈Z.
②∵f
k(x)=2
x-2k+3k,x∈(2k,2k+2],k∈Z是增函数,
∴Φ(x)的第k阶阶梯函数图象的最高点为P
k(2k+2,4+3k),
第k+1阶阶梯函数图象的最高点为P
k+1(2k+4,7+3k),
所以过P
k、P
k+1这两点的直线的斜率为k=
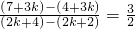
.同理可得过P
k+1、
P
k+2这两点的直线的斜率也为

.所以,Φ(x)的各阶阶梯函数图象的最高点共线.
(2)若Φ(x)=x
2,则f
k(x)=(x-2k)
2+3k,f
k(x)<(1-3k)x+4k
2+3k-1?(x-2k)
2+3k<(1-3k)x+4k
2+3k-1,
整理得出x
2-(k+1)x+1<0.当k=1时,x
2-2x+1<0无解,当k≥2时,x
2-(k+1)x+1<0,
得出
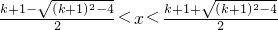
①
又根据x∈(2k,2k+2],k∈Z ②
又根据
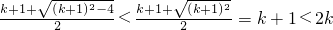
,①②无公共部分,即不存在正整数k满足题意.
分析:(1)利用题目中给出的阶梯函数的定义解决该类问题.关键要理解阶梯函数的定义以及一些字母和符号的含义.为求解函数解析式做准备,证明共线只需说明各点连线的斜率相等;
(2)掌握探究性问题的解决方法,要假设存在正整数,寻找相应的关系式进行求解或说明.
点评:本题考查新定义型问题的解决方法,属于创新题型.关键要理解阶梯函数的定义,然后写出该函数的解析式,利用单调性写出该函数的最值.掌握探究性问题的研究方法,先假设存在,再寻找字母满足的关系式,进行求解和判断.

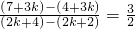 .同理可得过Pk+1、
.同理可得过Pk+1、 .所以,Φ(x)的各阶阶梯函数图象的最高点共线.
.所以,Φ(x)的各阶阶梯函数图象的最高点共线.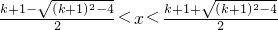 ①
①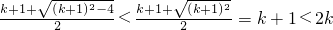 ,①②无公共部分,即不存在正整数k满足题意.
,①②无公共部分,即不存在正整数k满足题意.

