
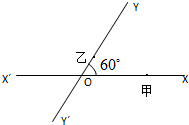
 如图,有两条相交成60°的直路XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后甲沿XX′方向用2km/h的速度,乙沿Y′Y方向用4km/h的速度同时步行.设t小时后甲在XX′上点A处,乙在YY′上点B处.
如图,有两条相交成60°的直路XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后甲沿XX′方向用2km/h的速度,乙沿Y′Y方向用4km/h的速度同时步行.设t小时后甲在XX′上点A处,乙在YY′上点B处.| 12+92-2×1×9×cos120° |
| 91 |
| 3 |
| 2 |
| (3-2t)2+(1+4t)2-2(3-2t)(1+4t)cos60° |
| 28t2-14t+7 |
| 3 |
| 2 |
| (2t-3)2+(1+4t)2-2(2t-3)(1+4t)cos120° |
| 28t2-14t+7 |
| 28t2-14t+7 |
| 28t2-14t+7 |
28(t-
|
| 1 |
| 4 |


科目:高中数学 来源:江苏省新星中学2008-2009学年度第二学期第三次月考高二数学试卷 题型:044
如图,有两条相交成60°角的直路![]() ,
,![]() ,交点是O,甲、乙分别在OX,OY上,起初甲离O点6 km,乙离O点2 km.后来甲沿
,交点是O,甲、乙分别在OX,OY上,起初甲离O点6 km,乙离O点2 km.后来甲沿![]() 的方向,乙沿
的方向,乙沿![]() 的方向,同时用4 km/h的速度步行.
的方向,同时用4 km/h的速度步行.

(1)t h后两人的距离是多少?
(2)什么时候两人的距离最短?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com