
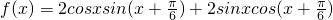 .
. 的值域;
的值域;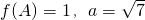 ,△ABC面积为
,△ABC面积为 .
.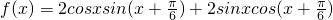 =2sin(2x+
=2sin(2x+ ),
), ]时,2x+
]时,2x+ ∈[
∈[ ,
, ],-
],- ≤sin(2x+
≤sin(2x+ )≤1,
)≤1, )=1,所以,sin(2A+
)=1,所以,sin(2A+ )=
)= ,所以A=
,所以A= .
. bcsinA=
bcsinA= bc=
bc= ,所以bc=6.
,所以bc=6. ),根据x的范围,求得角(2x+
),根据x的范围,求得角(2x+ )的正弦值,从而求得f(x)的值域.
)的正弦值,从而求得f(x)的值域. )=1,求得A的值,根据△ABC的面积S=
)=1,求得A的值,根据△ABC的面积S= ,求得bc的值,再由余弦定理求得b+c.
,求得bc的值,再由余弦定理求得b+c.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(理科)(解析版) 题型:解答题
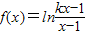 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(理科)(解析版) 题型:解答题
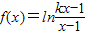 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(文科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期5月高考冲刺文科数学(解析版) 题型:解答题
(本小题满分12分)设函数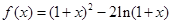 .
.
(I)求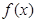 的单调区间;
的单调区间;
(II)当0<a<2时,求函数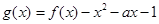 在区间
在区间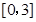 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源:2012年四川省泸州市高考数学一诊试卷(理科)(解析版) 题型:解答题
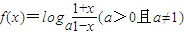 .
. 的值;
的值;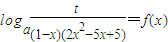 在x∈[0,1)上有实数解,求实数t的取值范围.
在x∈[0,1)上有实数解,求实数t的取值范围.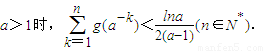 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com