练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

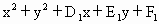    两圆：＝0及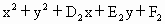：＝0，已知两圆相交于A、B两点，求公共弦AB所在直线的方程．

    答案：
    解析：

    　　解：可从这个二元二次方程组中解出两组解，但运算量太大．为避免这一繁点，可采取设而不求的办法，这正是曲线系方程在解题中如何运用的体现．

    　　设，则有：

    　　两式相减得：＝0．由A、B的可互换可知：此方程同时满足A、B两点．由两点确定一直线并直线与其方程的一一对应可知，此方程即是所求公共弦AB所在直线的方程．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习高手必修二数学苏教版 苏教版 题型：022

    过两圆x2＋y2＋2x＋3y－7＝0和x2＋y2＋3x－2y－1＝0的交点及点(1，2)的圆的方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在空间中,取直线l为轴,直线l′与l相交于O点,其夹角为α,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.任取平面π,若它与轴l交角为β（π与l平行,记β＝0）,则当?β＞α时,平面π与圆锥的交线为椭圆.试利用Dandelin双球（这两个球位于圆锥的内部,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥均相切）证明上述结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在空间中，取直线l为轴，直线l′与l相交于O点，其夹角为α，l′围绕l旋转得到以O为顶点，l′为母线的圆锥面，任取平面π，若它与轴l交角为β（π与l平行，记β＝0），则当β＞α时，平面π与圆锥的交线为椭圆.试利用Dandelin双球（这两个球位于圆锥的内部，一个位于平面π的上方，一个位于平面π的下方，并且与平面π及圆锥均相切）证明上述结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

           已知圆O：x2＋y2＝1，圆C：（x－4）2＋（y－4）2＝1，由两圆外一点P（a,b）引两圆切线PA、PB，切点分别为A、B，如图，满足|PA|＝|PB|；

           （Ⅰ）将两圆方程相减可得一直线方程l：x＋y－4=0，该直线叫做这两圆的“根轴”，试证点P落在根轴上；

           （Ⅱ）求切线长|PA|的最小值；

    （Ⅲ）给出定点M（0,2），设P、Q分别为直线l和圆O上动点，求|MP|＋|PQ|的最小值及此时点P的坐标．

    查看答案和解析>>

    同步练习册答案