
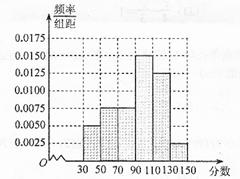
 和
和 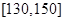 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在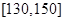 的有几人?
的有几人? 和
和 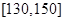 各1人的概率.
各1人的概率. .
.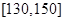 应抽取多少人;第三问,这问是对概率知识的考查,先把随机抽取的2人的所有情况一一列出,再挑选符合题意的情况,再求概率.
应抽取多少人;第三问,这问是对概率知识的考查,先把随机抽取的2人的所有情况一一列出,再挑选符合题意的情况,再求概率.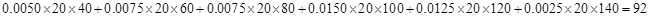 4分
4分 和
和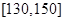 的人数分别为6人和3人,
的人数分别为6人和3人,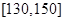 的人有
的人有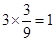 (人). 8分
(人). 8分 的有2人,记为
的有2人,记为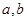 ,分数在
,分数在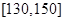 的人有1人,记为
的人有1人,记为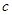 ,从中随机抽取2人,总的情形有
,从中随机抽取2人,总的情形有 三种.而分数在
三种.而分数在 和
和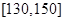 各1人的情形有
各1人的情形有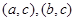 两种,故所求概率
两种,故所求概率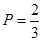 .
. 

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:不详 题型:解答题
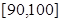 内的记为
内的记为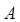 ,其中“语文”科目成绩在
,其中“语文”科目成绩在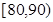 内的考生有10人.
内的考生有10人.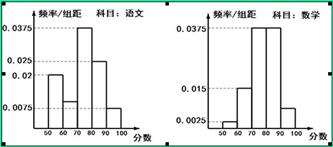
 的人数;
的人数;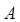 .在至少一科成绩为
.在至少一科成绩为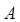 的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为
的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为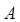 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 选择题 | 40 | 55 | 50 | 45 | 50 | 40 | 45 | 60 | 40 |
| 填空题 | 12 | 16 | 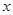 | 12 | 16 | 12 | 8 | 12 | 8 |
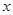 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、第2组
、第2组 、第3组
、第3组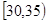 、第4组
、第4组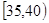 、第5组
、第5组 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示: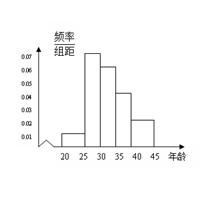
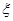 表示抽出的3名志愿者中第3组的人数,求
表示抽出的3名志愿者中第3组的人数,求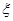 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |
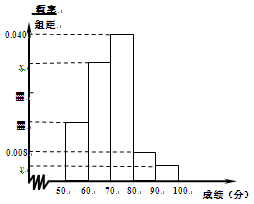
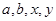 的值;
的值;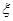 表示所抽取的2名同学中来自第5组的人数,求
表示所抽取的2名同学中来自第5组的人数,求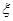 的分布列及其数学期望.
的分布列及其数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 非高收入族 | 高收入族 | 合计 |
| 赞成 | | | |
| 不赞成 | | | |
| 合计 | | | |

| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好; 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足 ;
; 和
和 ,它们的随机变量
,它们的随机变量 的观测值
的观测值 来说,
来说, 越小,认为“
越小,认为“ 和
和 有关系”的把握程度越大。
有关系”的把握程度越大。| A.①③ | B.②④ | C.③⑤ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 列联表:
列联表: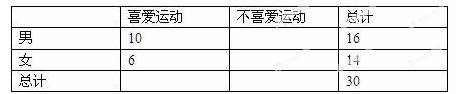
 (其中
(其中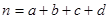 )
)| | 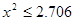 | 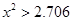 | 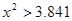 | 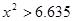 |
| 是否有关联 | 没有关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com