
北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为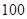 分,规定测试成绩在
分,规定测试成绩在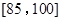 之间为体质优秀;在
之间为体质优秀;在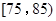 之间为体质良好;在
之间为体质良好;在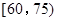 之间为体质合格;在
之间为体质合格;在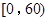 之间为体质不合格.
之间为体质不合格.
现从某校高三年级的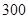 名学生中随机抽取
名学生中随机抽取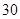 名学生体质健康测试成绩,其茎叶图如下:
名学生体质健康测试成绩,其茎叶图如下: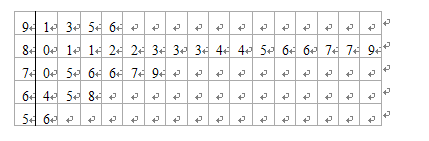
(Ⅰ)试估计该校高三年级体质为优秀的学生人数;
(Ⅱ)根据以上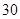 名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取
名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取 名学生,再从这
名学生,再从这 名学生中选出
名学生中选出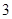 人.
人.
(ⅰ)求在选出的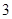 名学生中至少有
名学生中至少有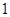 名体质为优秀的概率;
名体质为优秀的概率;
(ⅱ)求选出的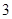 名学生中体质为优秀的人数不少于体质为良好的人数的概率.
名学生中体质为优秀的人数不少于体质为良好的人数的概率.
(Ⅰ)100;(Ⅱ)(ⅰ)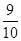 ,(ⅱ)
,(ⅱ)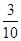
解析试题分析:(Ⅰ)由茎叶图可知抽取的30名学生中体质优秀的有10人,所以优秀率为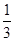 ,用总数乘以优秀率即可得优秀的总人数。(Ⅱ)由茎叶图可知抽取的30名学生中体质优秀的有10人,体质为良好的15人。所以样本中体质为优秀和良好的学生的比为
,用总数乘以优秀率即可得优秀的总人数。(Ⅱ)由茎叶图可知抽取的30名学生中体质优秀的有10人,体质为良好的15人。所以样本中体质为优秀和良好的学生的比为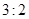 。分层抽样的特点是在各层按比例抽取,所以抽取的5人中有3人体质为良好有2人体质为优秀。(ⅰ)和(ⅱ)中的概率均属古典概型,用例举法分别求基本事件总数和所求事件包含的基本事件数即可。
。分层抽样的特点是在各层按比例抽取,所以抽取的5人中有3人体质为良好有2人体质为优秀。(ⅰ)和(ⅱ)中的概率均属古典概型,用例举法分别求基本事件总数和所求事件包含的基本事件数即可。
试题解析:解:(Ⅰ)根据抽样,估计该校高三学生中体质为优秀的学生人数有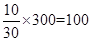 人. 3分
人. 3分
(Ⅱ)依题意,体质为良好和优秀的学生人数之比为  .
.
所以,从体质为良好的学生中抽取的人数为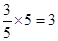 ,从体质为优秀的学生中抽取的人数为
,从体质为优秀的学生中抽取的人数为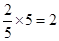 . 6分
. 6分
(ⅰ)设在抽取的 名学生中体质为良好的学生为
名学生中体质为良好的学生为 ,
,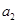 ,
, ,体质为优秀的学生为
,体质为优秀的学生为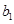 ,
,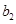 .
.
则从 名学生中任选
名学生中任选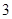 人的基本事件有
人的基本事件有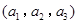 ,
,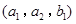 ,
,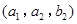 ,
,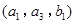 ,
,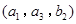 ,
,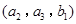 ,
,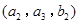 ,
,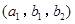 ,
,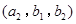 ,
,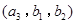
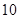 个,其中“至少有
个,其中“至少有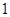 名学生体质为优秀”的事件有
名学生体质为优秀”的事件有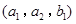 ,
,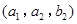 ,
,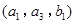 ,
,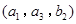 ,
,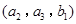 ,
,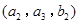 ,
,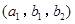 ,
, 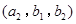 ,
,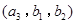
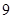 个.
个.
所以在选出的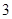 名学生中至少有
名学生中至少有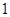 名学生体质为优秀的概率为
名学生体质为优秀的概率为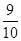 . 10分
. 10分
(ⅱ)“选出的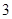 名学生中体质为优秀的人数不少于体质为良好的人数”的事件有
名学生中体质为优秀的人数不少于体质为良好的人数”的事件有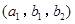 ,
,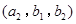 ,
,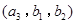
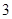 个.
个.
所以选出的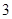 名学生中体质为优秀的人数不少于体质为良好的人数的概率为
名学生中体质为优秀的人数不少于体质为良好的人数的概率为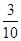 .13分
.13分
考点:1分层抽样;2古典概型.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
| API | 0~50 | 51~ 100 | 101~ 150 | 151~ 200 | 201~ 250 | 251~ 300 | >300 |
| 级 别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状 况 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
| |  |  |  |  |  | ||

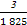 +
+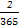 +
+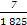 +
+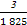 +
+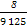 =
=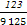 ,365=73×5).
,365=73×5).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,
8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.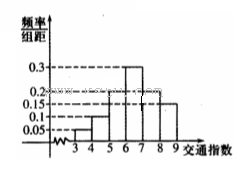
(1)这20个路段轻度拥堵、中度拥堵的路段各有多少个?
(2)从这20个路段中随机抽出的3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.
(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?
(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由某种设备的使用年限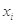 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得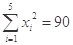 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费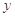 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与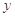 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中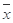 ,
, 为
为
样本平均值,线性回归方程也可写为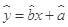 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两名同学参加“汉字听写大赛”选拔性测试.在相同的测试条件下,两人5次测试的成绩(单位:分)如下表:
(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算);
(Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,求抽到的两个成绩中至少有一个高于
90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校900名学生在一次百米测试中,成绩全部介于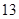 秒与
秒与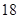 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组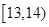 ,第二组
,第二组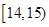 ,…,第五组
,…,第五组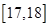 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.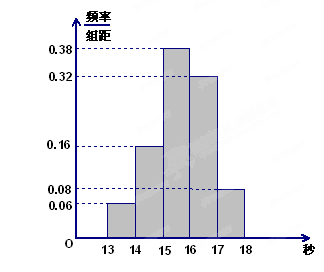
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计学校900名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数(保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出 与销售额
与销售额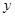 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
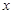 | 2 | 4 | 5 | 6 | 8 |
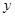 | 30 | 40 | 60 | 50 | 70 |
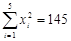


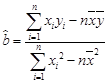 ,
, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com