Question

【题目】数列{an}是公比为q（q＞1）的等比数列，其前n项和为Sn ． 已知S3=7，且3a2是a1+3与a3+4的等差数列． （Ⅰ）求数列{an}的通项公式an；
（Ⅱ）设bn= ，cn=bn（bn+1﹣bn+2），求数列{cn}的前n项和Tn ．

Answer 1

【答案】解：（Ⅰ）依题意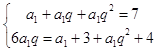， ，解得： ， ∴数列{an}的通项公式an=2n﹣1；
（Ⅱ）∵bn= = ，cn=bn（bn+1﹣bn+2）= （ ﹣ ）=（ ﹣ ）﹣ （ ﹣ ），
∴Tn=c1+c2+…+cn=[（1﹣ ）﹣ （ ﹣ ）]+[（ ﹣ ）﹣ （ ﹣ ）]+…+[（ ﹣ ）﹣ （ ﹣ ）]
=（1﹣ ）﹣ （1﹣ + ﹣ + ﹣ +…+ ﹣ ）
= ﹣ （1+ ﹣ ﹣ ）
= ﹣ ．
【解析】（Ⅰ）依题意，可得， ，解得首项与公比，即可求得等比数列{an}的通项公式an；（Ⅱ）由an=2n﹣1可得bn= = ，cn=bn（bn+1﹣bn+2）=（ ﹣ ）﹣ （ ﹣ ），利用裂项法与分组求和法即可求得数列{cn}的前n项和Tn ．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系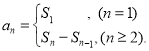)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．