
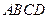 和
和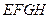 构成的面积为
构成的面积为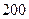 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形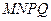 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为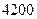 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为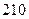 元/m2,再在四个空角(如
元/m2,再在四个空角(如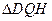 等)上铺草坪,造价为
等)上铺草坪,造价为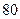 元/m2. 设总造价为
元/m2. 设总造价为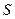 元,
元,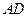 长为
长为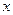 m.
m.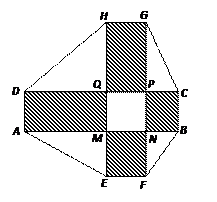 (1)用
(1)用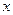 表示矩形
表示矩形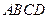 的边
的边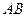 的长
的长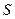 与
与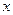 的函数关系
的函数关系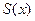
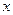 为何值时,
为何值时,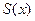 最小?并求这个最小值
最小?并求这个最小值 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:不详 题型:解答题
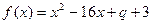 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
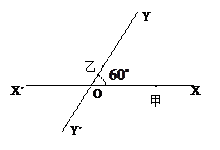
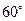 的直路
的直路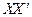 ,
,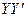 ,交点是
,交点是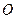 ,甲、乙分别在
,甲、乙分别在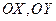 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿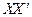 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿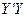 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在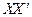 上点A处,乙在
上点A处,乙在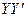 上点B处.
上点B处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com