
在三角形ABC中,下列等式总能成立的是( )
A. a cosC=c cosA B. bsinC=csinA C. absinc=bcsinB D. asinC=csinA
D
【解析】
试题分析:A:由正弦定理可得,acosC-ccosA=2RsinAcosC-2RsinCcosA=2Rsin(A-C)=0不一定成立,
即acosC=ccosA 不一定成立,A错误
B:由正弦定理可得,bsinC-csinA=2RsinBsinC-2RsinCsinA=2RsinC(sinB-sinC)=0不一定成立,即bsinC=csinA不一定成立,B错误
C:由正弦定理可得absinC-bcsinB=2bR(sinAsinC-sinCsinB)=2bRsinC(sinA-sinB)=0不一定成立,即absinC=bcsinB不一定成立,C错误
D:由正弦定理可得,asinC-csinA=2RsinAsinC-2RsinCsinA=0,即asinC=csinA一定成立,D正确
故选D
考点:本题主要考查正弦定理、余弦定理的应用。
点评:利用正弦定理、余弦定理对选项进行分析。


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:湖南部分中学2007年4月高三调研联考数学理科 题型:044
在三角形ABC中,A、B、C所对的边分别为a、b、c,且![]()
方程节(下一个)
(1)求A的大小;(2)若a=查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三三月月考数学(理)试卷 题型:解答题
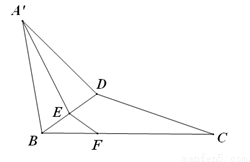
如图:在直角三角形ABC中,已知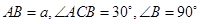 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角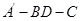 的大小记为
的大小记为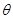 .
.
⑴求证:平面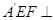 平面BCD;
平面BCD;
⑵当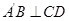 时,求
时,求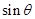 的值;
的值;
⑶在⑵的条件下,求点C到平面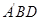 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
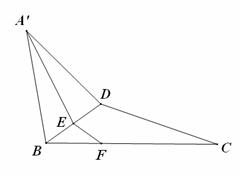
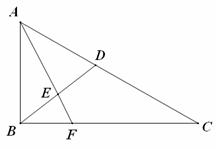
如图:在直角三角形ABC中,已知![]() , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角![]() 的大小记为
的大小记为![]() .
.
⑴求证:平面![]() 平面BCD;
平面BCD;
⑵当![]() 时,求
时,求![]() 的值;
的值;
⑶在⑵的条件下,求点C到平面![]() 的距离.
的距离.
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com