
定义在[-1,1]上的奇函数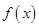 满足
满足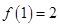 ,且当
,且当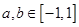 ,
,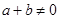 时,有
时,有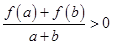 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若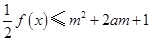 对所有
对所有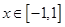 ,
,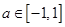 恒成立,
恒成立,
求实数m的取值范围.
(1)根据函数单调性的定义,设变量作差变形定号下结论。
(2)实数m的取值范围是 或
或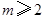 或
或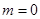 .
.
【解析】
试题分析:解:(1)假设函数的图象上存在两个满足条件的点A,B,则它们的纵坐标相同
任取 ,且
,且 , 则
, 则
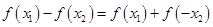
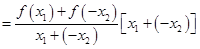 4分
4分
因为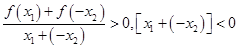 ,
,
所以,
∴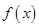 是[-1,1]上的增函数 6分
是[-1,1]上的增函数 6分
这与假设矛盾,所以假设不成立,
∴ 函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直 8分
(2)要使得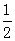
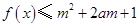 对所有
对所有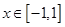 ,
,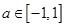 恒成立,
恒成立,
只须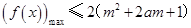 , 11分
, 11分
由(1)得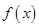 是[-1,1]上的增函数 ∴
是[-1,1]上的增函数 ∴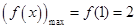
∴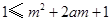 对任意的
对任意的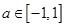 恒成立 3分
恒成立 3分
令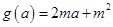 ,则只须
,则只须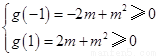 ,
,
解之得: 或
或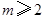 或
或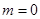 15分
15分
∴实数m的取值范围是 或
或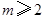 或
或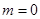 . 16分
. 16分
考点:函数的奇偶性和单调性
点评:解决的关键是利用单调性的定义证明,同事利用不等式恒成立来化简为分离参数的思想来求解最值得到参数的范围。


科目:高中数学 来源: 题型:
| ax+b |
| x2+1 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
判断函数f(x)在[-1,1]上是增函数还是减函数,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com