
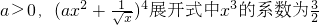 ,则a=________;
,则a=________;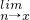 (a+a2+…an)=________.
(a+a2+…an)=________. 1
1 )r,整理后,令x的次数等于3,从而解得a,
)r,整理后,令x的次数等于3,从而解得a, <1,可知数列a,a2…an是递降等比数列,则
<1,可知数列a,a2…an是递降等比数列,则  (a+a2+…+an)表示无穷递降等比数列的各项和,利用无穷递降等比数列的各项和公式,可得解.
(a+a2+…+an)表示无穷递降等比数列的各项和,利用无穷递降等比数列的各项和公式,可得解. )r,整理得Tr+1=c4ra4-rx8-
)r,整理得Tr+1=c4ra4-rx8- r,
r, ,∴a=
,∴a= .
. .
. ,可知数列a,a2…an是递降等比数列,
,可知数列a,a2…an是递降等比数列, (a+a2+…+an)表示无穷递降等比数列的各项和,
(a+a2+…+an)表示无穷递降等比数列的各项和, sn=
sn= ),
), (a+a2+…+an)=
(a+a2+…+an)=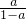 ═
═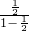 =1.
=1. an=0,要记住无穷递降等比数列各项和公式
an=0,要记住无穷递降等比数列各项和公式  sn=
sn= .在选择填空中可以加快速度.
.在选择填空中可以加快速度. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com