

图2-4-16
(1)试判断△DCT的形状.
(2)△DCT有无可能成为正三角形?若无可能,说明为什么;若有可能,求出这时PB与PA应满足的条件.
思路分析:要判断△DCT的形状,先考虑其内角的关系,注意到CT、CB为切线,则连结BT,可用弦切角定理推论得∠ATB =∠BTD =90°,从而可判断△DCT的形状.

解:(1)连结BT,∵CB、CT为⊙O的切线,?
∴∠CTB =CBT.?
又AB为⊙O的直径,∴∠ATB =∠DTB =90°.?
∴∠DTC =90°-∠CTB,
∠D =90°-∠CBT.?
∴∠DTC =∠D,即CD =CT.?
∴△DCT为等腰三角形.?
(2)若△DCT为正三角形,则∠D =60°,?
由(1)知∠CBT=90°-∠D =30°,?
而CB切⊙O于B,?
∴∠A =∠CBT=30°.?
∴在Rt△ATB中,![]() =sin30°=
=sin30°=![]() ,?
,?
且∠ABT=90°-30°=60°,∠ABT =∠CTB +∠P.?
而∠CTB =∠CBT =30°,?
∴∠P =30°.∴∠P =∠CTB.?
∴PB = TB.∴![]() =
=![]() ,?
,?
即当PB∶PA=1∶3时,△DCT为正三角形.


科目:高中数学 来源: 题型:
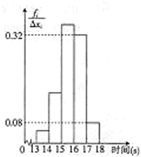 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:044

图1-3-16
求证:(1)GH·CE =DF·BC;?
(2)DC2=DF·DE;?
(3)CH·CD =GH·DE;?
(4)GB∶BA =CH∶BH;?
(5)CH·EF =BA·DF.
查看答案和解析>>
科目:高中数学 来源: 题型:
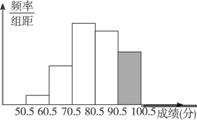
(1)求第五小组的频率,并补全频率分布直方图;
(2)求竞赛成绩大于80.5分且小于90.5分的学生数;
查看答案和解析>>
科目:高中数学 来源: 题型:
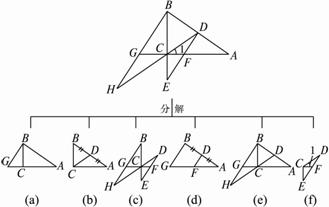
图1-3-16
求证:(1)GH·CE =DF·BC;
(2)DC2=DF·DE;
(3)CH·CD =GH·DE;
(4)GB∶BA =CH∶BH;
(5)CH·EF =BA·DF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com