
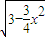 的图象上至少存在不同的三点到(1,0)的距离构成等比数列,则公比的取值范围 .
的图象上至少存在不同的三点到(1,0)的距离构成等比数列,则公比的取值范围 . 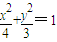 的上半部分,而点F(1,0)恰好是椭圆的右焦点.设图象上有三个点P1、P2、P3满足P1F、P2F、P3F构成等比数列,且公比为q,可得
的上半部分,而点F(1,0)恰好是椭圆的右焦点.设图象上有三个点P1、P2、P3满足P1F、P2F、P3F构成等比数列,且公比为q,可得 =q2.最后根据椭圆上一点到焦点距离的最大、最小值,讨论得到公比q的取值范围.
=q2.最后根据椭圆上一点到焦点距离的最大、最小值,讨论得到公比q的取值范围.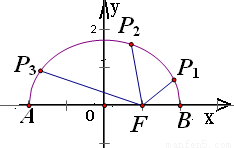 解:将函数函数y=
解:将函数函数y= 化简,整理得
化简,整理得 ,其中y≥0
,其中y≥0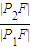 =
= =q,所以
=q,所以 =q2
=q2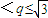
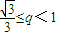
 或
或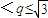
 ,1)∪(1,
,1)∪(1, ]
]

 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
| 4-(x-3)2 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、(0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com