
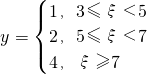 ,从该厂生产的产品中任取一件,其利润记为X,用这个样本的频率分布估计总体分布,将频率视为概率,求X的分布列和数学期望.
,从该厂生产的产品中任取一件,其利润记为X,用这个样本的频率分布估计总体分布,将频率视为概率,求X的分布列和数学期望.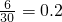 ,故估计该厂生产的产品的一等品率为0.2--------(4分)
,故估计该厂生产的产品的一等品率为0.2--------(4分)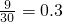 ,故估计该厂生产的产品的二等品率为0.3;--------------(5分)
,故估计该厂生产的产品的二等品率为0.3;--------------(5分)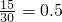 ,故估计该厂生产的产品的三等品的频率为0.5.----------(6分)
,故估计该厂生产的产品的三等品的频率为0.5.----------(6分)| X | 1 | 2 | 4 |
| P(X) | 0.5 | 0.3 | 0.2 |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:

|
查看答案和解析>>
科目:高中数学 来源: 题型:
 某产品按行业生产标准分成8个等级,等级系数ξ依次为1,2,…,8,产品的等级系数越大表明产品的质量越好,现从某厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如图:
某产品按行业生产标准分成8个等级,等级系数ξ依次为1,2,…,8,产品的等级系数越大表明产品的质量越好,现从某厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如图:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com