
分析 (1)先求出曲线C1的直角坐标方程,再由x=ρcosθ,y=ρsinθ,能求出到C1的极坐标方程.
(2)将ρ=-2sinθ代入ρ2+8ρcosθ+10ρsinθ+16=0,得sin(2θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,由此能求出C1与C2交点的极坐标.
解答 解:(1)∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=-4+5cost}\\{y=-5+5sint}\end{array}\right.$(t为参数),
∴曲线C1的直角坐标方程为(x+4)2+(y+5)2=25,
∴x=ρcosθ,y=ρsinθ,
∴(ρcosθ+4)2+(ρsinθ+5)2=25,
化简,得到C1的极坐标方程为:ρ2+8ρcosθ+10ρsinθ+16=0.
(2)将ρ=-2sinθ代入ρ2+8ρcosθ+10ρsinθ+16=0,
化简,得:sin2θ+sinθcosθ-1=0,
整理,得sin(2θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
∴2θ-$\frac{π}{4}$=2kπ+$\frac{π}{4}$或$2θ-\frac{π}{4}$=2kπ+$\frac{3π}{4}$,k∈Z,
由ρ≥0,0≤θ<2π,得$θ=\frac{5π}{4}$或$θ=\frac{3π}{2}$,
代入ρ=-2sinθ,得$\left\{\begin{array}{l}{θ=\frac{5π}{4}}\\{ρ=\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{θ=\frac{3π}{2}}\\{ρ=2}\end{array}\right.$,
∴C1与C2交点的极坐标为($\sqrt{2}$,$\frac{5π}{4}$)或(2,$\frac{3π}{2}$).
点评 本题考查参数方程与极坐标方程的互化,考查曲线的交点的极坐标的求法,是中档题,解题时要认真审题,注意直角坐标方程与极坐标方程互化公式的合理运用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x>1} | C. | R | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
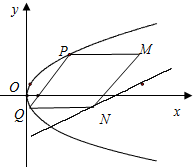 抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),
抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={log_2}(\sqrt{{x^2}+1}-x)$ | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=x2-x3 | D. | f(x)=sinx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com