练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    连接平行四边形ABCD的一个顶点至AD、DC边中点E、F，BE、BF分别与AC交于R、T两点，研究性学习小组在几何画板上拖动平行四边形的顶点时动态观察发现：

    ①＝＝保持不变；②＝(＋)；③△BRT是等边三角形

    上述观察对任意平行四边形成立的是

    [　　]

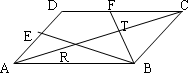
    A．①②

    B．①③

    C．②③

    D．①

    答案：A
    解析：

    不论平行四边形的形状如何改变，①②对任意平行四边形均成立，③不成立


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在正三棱柱ABC-A1B1C1中，E∈BB1，截面A1EC⊥侧面AC1．
    精英家教网
    （1）求证：BE=EB1；
    （2）若AA1=A1B1；求平面A1EC与平面A1B1C1所成二面角（锐角）的度数．
    注意：在下面横线上填写适当内容，使之成为（Ⅰ）的完整证明，并解答（Ⅱ）．
    精英家教网
    （1）证明：在截面A1EC内，过E作EG⊥A1C，G是垂足．
    ①∵
     

    ∴EG⊥侧面AC1；取AC的中点F，连接BF，FG，由AB=BC得BF⊥AC，
    ②∵
     

    ∴BF⊥侧面AC1；得BF∥EG，BF、EG确定一个平面，交侧面AC1于FG．
    ③∵
     

    ∴BE∥FG，四边形BEGF是平行四边形，BE=FG，
    ④∵
     

    ∴FG∥AA1，△AA1C∽△FGC，
    ⑤∵
     

    ∴FG=
    1
    2
    AA1=
    1
    2
    BB1    ，即BE=
    1
    2
    BB1，故BE=EB1    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

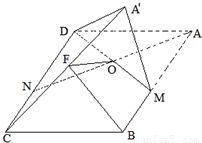
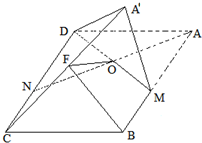    如图，在平行四边形ABCD中，AB=2BC=2，∠ABC=120°．M、N分别为线段AB，CD的中点，连接AN，DM交于点O，将△ADM沿直线DM翻折成△A'DM，使平面A'DM⊥平面BCD，F为线段A'C的中点．
    （1）求证：ON⊥平面A'DM
    （2）求证：BF∥平面A'DM；
    （3）直线FO与平面A'DM所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

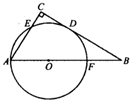    （2012•大连二模）任选一题作答选修：几何证明选讲如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆与BC相切于点D，分别交AC、AB于点E、F．
    （I）若AC=6，AB=10，求⊙O的半径；
    （Ⅱ）连接OE、ED、DF、EF．若四边形BDEF是平行四边形，试判断四边形OFDE的形状，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

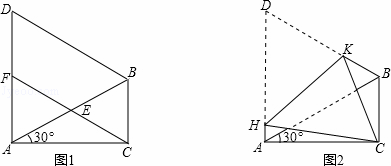
    如图1，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD于F．

    （1）求证：①△AEF≌△BEC；②四边形BCFD是平行四边形；

    （2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，求sin∠ACH的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年广东省汕头市金山中学高三（上）开学摸底数学试卷（理科）（解析版） 题型：解答题

    如图，在平行四边形ABCD中，AB=2BC=2，∠ABC=120°．M、N分别为线段AB，CD的中点，连接AN，DM交于点O，将△ADM沿直线DM翻折成△A'DM，使平面A'DM⊥平面BCD，F为线段A'C的中点．
    （1）求证：ON⊥平面A'DM
    （2）求证：BF∥平面A'DM；
    （3）直线FO与平面A'DM所成的角．

    查看答案和解析>>

    同步练习册答案