
分析 (Ⅰ)求出函数的导数,解关于导函数的方程求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)当x>0时,有$k=\frac{e^x}{x^2}$,令$h(x)=\frac{e^x}{x^2}$,根据函数的单调性求出k的范围即可.
解答 解:(Ⅰ)f'(x)=ex-2,
令f'(x)=0解得x=ln2,
易知f(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,
故当x=ln2时,f(x)有极小值f(ln2)=2-2ln2.…(5分)
(Ⅱ)方程f(x)=ex-2x=kx2-2x,整理得ex=kx2,
当x>0时,$k=\frac{e^x}{x^2}$.…(6分)
令$h(x)=\frac{e^x}{x^2}$,则$h'(x)=\frac{{{e^x}•{x^2}-{e^x}•2x}}{x^4}=\frac{{{e^x}(x-2)}}{x^3}$,…(8分)
令h'(x)=0,解得x=2,
易得h(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
所以x=2时,φ(x)有最小值$φ(2)=\frac{e^2}{4}$,.…(10分)
而当x越来越靠近0时,φ(x)的值越来越大,
又当x>0,方程f(x)=kx2-2x无解,
所以$k<\frac{e^2}{4}$..…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$)(k∈Z) | B. | (kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$)(k∈Z) | ||
| C. | (2kπ+$\frac{π}{3}$,2kπ+$\frac{4π}{3}$)(k∈Z) | D. | (2kπ-$\frac{π}{3}$,2kπ+$\frac{π}{6}$)(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,16} | B. | {0,1} | C. | {1,16} | D. | {0,1,4,16} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
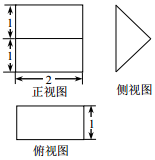 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 4 | B. | $6+4\sqrt{2}$ | C. | $4+4\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在回归分析模型中,残差平方和越大,说明模型的拟合效果越好 | |
| B. | 线性相关系数|r|越大,两个变量的线性相关性越强;反之,线性相关性越弱 | |
| C. | 由变量x和y的数据得到其回归直线方程l:$\widehat{y}$=$\widehat{b}$x+a,则l一定经过P($\overline{x}$,$\overline{y}$) | |
| D. | 在回归直线方程$\widehat{y}$=0.1x+1中,当解释变量x每增加一个单位时,预报变量$\widehat{y}$增加0.1个单位. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com