
已知点A(2,2)和直线l∶3x+4y-20=0.求
(1)过点A和直线l平行的直线方程;
(2)过点A和直线l垂直的直线方程.
思路分析:本题可依题意求出所求直线的斜率后用点斜式求解,也可利用直线系方程的方法来求解.
(1)解法一:利用直线方程的点斜式求解.
由l∶3x+4y-20=0,得k1=![]() .
.
设过A点且平行于l的直线为l1,则k11=k1=![]() ,所以l1的方程为
,所以l1的方程为
y-2=![]() (x-2),即3x+4y-14=0.
(x-2),即3x+4y-14=0.
解法二:利用直线系方程求解.
设过点A且平行于直线l的直线l1的方程为3x+4y+m=0.
由点A(2,2)在直线l1上,得3×2+4×2+m=0,解得m=-14.
故直线l1的方程为3x+4y-14=0.
(2)解法一:设过点A与l垂直的直线为l2.
因为k1·k12=-1,所以k12=![]() ,故直线l2的方程为y-2=
,故直线l2的方程为y-2=![]() (x-2),即4x-3y-2=0.
(x-2),即4x-3y-2=0.
解法二:设l2的方程为4x-3y+m=0.
因为l2经过点A(2,2),所以4×2-3×2+m=0,解得m=-2.故l2的方程为4x-3y-2=0.
(1)经过点A(x0,y0)与直线l∶Ax+By+C=0平行或垂直的直线方程,当l的斜率存在(垂直时,要求斜率不为零)时,可利用直线方程的点斜式求直线方程,也可利用待定系数法根据直线系方程求直线方程.
(2)称Ax+By+m=0是与直线Ax+By+C=0平行的直线系方程(其中m≠C).当m=C时,直线Ax+By+m=0与直线Ax+By+C=0重合.称?Bx-Ay+m=0为与直线Ax+By+C=0垂直的直线系方程,其中参数m为任意实数.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:学习高手必修二数学苏教版 苏教版 题型:044
已知点A(2,2)和直线l:3x+4y-20=0,求:
(1)过A点和直线l平行的直线方程.
(2)过A点和直线l垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源:新课程高中数学疑难全解 题型:044
已知点A(2,2)和椭圆方程![]() +
+![]() =1的右焦点F2(4,0),M为椭圆上的动点.
=1的右焦点F2(4,0),M为椭圆上的动点.
(1)求|MA|+|MF2|的最值;
(2)求|MA|+![]() |MF2|的最小值.
|MF2|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
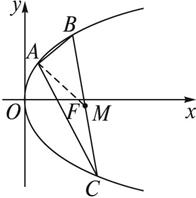
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC的中点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com