
已知:正方体
ABCD-A1B1C1D1棱长为a.(1)求证:平面A1BD∥平面B1D1C;
(2)求平面A1BD和平面B1D1C的距离.
|
证明: (1)在正方体ABCD-A1B1C1D1中,∵ BB1平行且等于DD1,∴四边形 BB1D1D是平行四边形,∴ BD∥B1D1,∴ BD∥平面B1D1C.同理A1B∥平面B1D1C, 又A1B∩BD=B, ∴平面A1BD∥平面B1D1C
解: (2)连AC1交平面A1BD于M,交平面B1D1C于N.AC是AC1在平面AC上的射影,又AC⊥BD, ∴ AC1⊥BD,同理可证, AC1⊥A1B,∴ AC1⊥平面A1BD,即MN⊥平面A1BD,同理可证 MN⊥平面B1D1C.∴MN的长是平面A1BD到平面B1D1C的距离, 设AC、BD交于E,则平面A1BD与平面A1C交于直线A1E. ∵M∈平面A1BD,M∈AC1 ∴M∈A1E. 同理N∈CF. 在矩形AA1C1C中,见下图,由平面几何知识得 ∴
评述:当空间图形较为复杂时,可以分解图形,把其中的平面图形折出分析,利于清楚地观察出平面上各种线面的位置关系.证明面面平行,主要是在其中一个平面内找出两条与另一个平面平行的相交直线,或者使用反证法. |


科目:高中数学 来源: 题型:
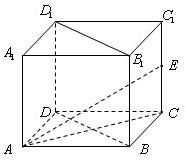 已知:正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点.
已知:正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知单位正方体ABCD-A1B1C1D1,E分别是棱C1D1的中点,试求:
已知单位正方体ABCD-A1B1C1D1,E分别是棱C1D1的中点,试求:查看答案和解析>>
科目:高中数学 来源: 题型:
 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.
(2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com