
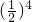 =
= …(4分)
…(4分)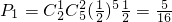 ,
,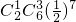 =
= ,由于两种情况互斥,
,由于两种情况互斥, ,∴获利不低于1200万美元的概率为
,∴获利不低于1200万美元的概率为 .…(8分)
.…(8分)| ξ | 800 | 1000 | 1200 | 1400 |
P |  |  |  |  |
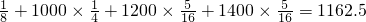 (万美元) …(12分)
(万美元) …(12分) ,两队都有可能胜,利用相互独立事件的概率乘法公式求其概率即可;
,两队都有可能胜,利用相互独立事件的概率乘法公式求其概率即可;

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:浙江省杭州市学军中学2007-2008学年度第一学期期中考试高三数学试题(理) 题型:044
美国蓝球NBA总决赛采用7场4胜制,即若某队先取胜4场则比赛结束.已知某年参加总决赛的为甲,乙两队,在每场比赛中两队获胜的概率均为![]() .而每主办一场比赛,组织者有望获取收益2000万美元.求:
.而每主办一场比赛,组织者有望获取收益2000万美元.求:
(1)所需比赛场数ξ的分布列;
(2)组织者收益的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
美国篮球NBA总决赛采用7场4胜制,即若某队先取胜4场则比赛结束。已知某年参加总决赛的为甲,乙两队,在每场比赛中两队获胜的概率均为![]() 。而每主办一场比赛,组织者有望获取收益2000万美元. 求:
。而每主办一场比赛,组织者有望获取收益2000万美元. 求:
(1)所需比赛场数![]() 的分布列;
的分布列;
(2)组织者收益的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com