Question

设抛物线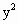＝2p(x＋)(p＞0)的准线和焦点分别是双曲线的右准线和右焦点，直线y＝kx与抛物线及双曲线在第一象限分别交于点A、B，且A为OB的中点,O为坐标原点)．

　　

(Ⅰ)当k＝时，求双曲线渐近线的斜率；

(Ⅱ)在(Ⅰ)的条件下，若双曲线的一条渐近线在y轴上的截距为，求抛物线和双曲线的方程；

(Ⅲ)设抛物线的顶点为M，抛物线与直线的另一交点为C，是否存在实数k，使得△ACM的面积等于直线MA、MC的斜率翟乘积的绝对值？若存在，求出k值，若不存在，请说明理由．

Answer 1

答案：
解析：

解(1)将y＝x代入，解得点A的坐标为(p，2p)． 　　∵A是OB的中点，∴点B的坐标为(3p，4p)． 　　设点B到准线的距离为BH，则由双曲线定义，得 　　e＝． 　　∴双曲线渐近线的斜率为． 　　(2)设双曲线中心为(－c，0)，则双曲线的一条渐近线方程为 　　y＝(x＋c)． 　　令x＝0，得； 　　∴c＝5，a＝4，b＝3． 　　∴双曲线方程为＝1 　　又双曲线的右准线为x＝－p，－p＋5＝． 　　∴抛物线方程为 　　(3)抛物线的顶点坐标为(－，0)． 　　设直线与抛物线的交点坐标为A()，C()．联立方程组 　　 　　． 　　则＝－4， 　　 　　　　 ＝ 　　　　 ＝． 　　由题意知：． 　　∴当64－＞0，即0＜p＜时，存在满足题设条件的实数k＝±； 　　当64－≤0时，k不存在．