
如图(1)在正方形SG1G2G3中,E、F分别是边G1G2、G2G3的中点,沿SE、SF及EF把这个正方形折成一个几何体如图(2),使G1,G2,G3三点重合于G,下面结论成立的是

SG⊥平面EFG
SD⊥平面EFG
GF⊥平面SEF
DG⊥平面SEF
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源:2012届河南郑州市高二下学期第二次月考试题数学(文科) 题型:选择题
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( ).

A.1:3 B.1:4
C.1:5 D.1:6
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由. W ww.k s 5u.c om


查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由. W ww.k s 5u.c om
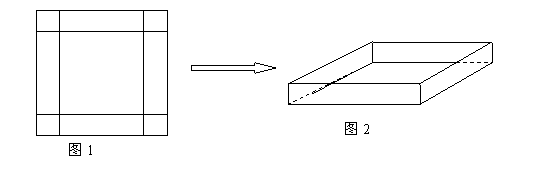

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com