
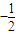 ,0),B(
,0),B(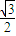 ,0,0),D(0,2,0),这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
,0,0),D(0,2,0),这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可. ,则
,则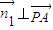 ,
,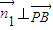 ,设平面PDB的法向量为
,设平面PDB的法向量为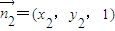 ,则
,则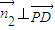 ,
,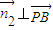 ,所以所求二面角的大小即为这两个法向量的夹角的大小.
,所以所求二面角的大小即为这两个法向量的夹角的大小.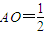 ,
,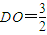 ,
,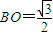 .
.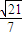 ,
,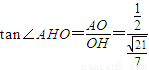 =
=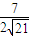 .
.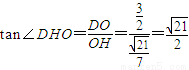 ;
;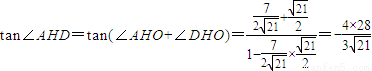 =
=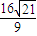
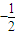 ,0),B(
,0),B(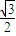 ,0,0),D(0,2,0),
,0,0),D(0,2,0),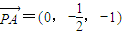 ,
,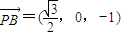 ,
,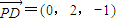
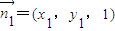 ,则
,则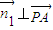 ,
,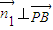 ,
,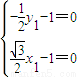 ,
,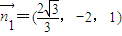 ;
;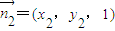 ,则
,则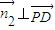 ,
,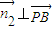 ,
,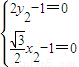 ,
,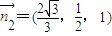 ;
;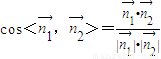 =
=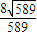


科目:高中数学 来源: 题型:
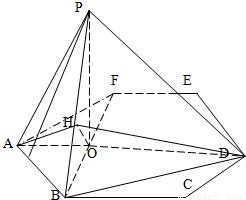
 如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1,
如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1,查看答案和解析>>
科目:高中数学 来源: 题型:
(06年安徽卷)(12分)
如图,P是边长为1的正六边形ABCDEF所在平面外一点,![]() ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明![]() ⊥
⊥![]() ;
;
(Ⅱ)求面![]() 与面
与面![]() 所成二面角的大小。
所成二面角的大小。

查看答案和解析>>
科目:高中数学 来源: 题型:
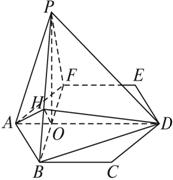
(1)证明PA⊥BF;
(2)求面APB与面DPB所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源:2006年普通高等学校招生全国统一考试安徽卷数学理科 题型:解答题
(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点,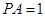 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明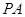 ⊥
⊥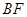 ;
;
(Ⅱ)求面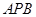 与面
与面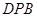 所成二面角的大小。
所成二面角的大小。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com