
如图,在四棱锥P-ABCD中,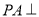 平面ABCD,AD//BC,
平面ABCD,AD//BC,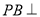 AC,
AC,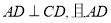
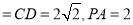 ,点M在线段PD上.
,点M在线段PD上.
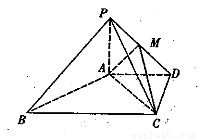
(1)求证: 平面PAC;
平面PAC;
(2)若二面角M-AC-D的大小为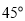 ,试确定点M的位置.
,试确定点M的位置.
(1)详见解析;(2)点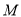 为线段
为线段 的中点.
的中点.
【解析】
试题分析:(1)要证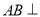 平面
平面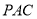 ,只要证:
,只要证: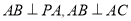 ,由题设
,由题设 平面
平面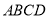
得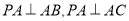 ,结合条件
,结合条件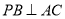 ,可证
,可证 平面
平面 ,从而有
,从而有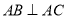 ,结论可证.
,结论可证.
(2)以 为坐标原点,
为坐标原点, 分别为
分别为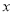 轴,
轴,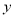 轴,
轴,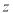 轴建立空间直角坐标系
轴建立空间直角坐标系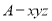 如图所示
如图所示
写出相关点的坐标,求出平面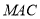 和平面
和平面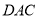 的法向量,利用向量的夹角公式求出点
的法向量,利用向量的夹角公式求出点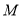 的坐标,从而确定点M的位置.
的坐标,从而确定点M的位置.
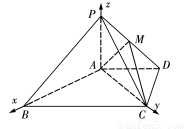
解证:(1)因为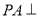 平面
平面 ,
,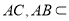 平面
平面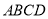
所以  ,
,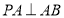 2分
2分
又因为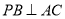 ,
, ,
,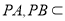 平面
平面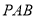 ,
,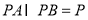 ,
,
所以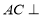 平面
平面 3分
3分
又因为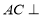 平面
平面 ,
, 平面
平面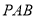 ,
,
所以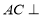
 4分
4分
因为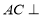
 ,
,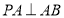 ,
, 平面
平面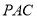 ,
,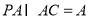 ,
,
所以 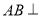 平面
平面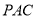 6分
6分
(2)因为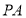 ⊥平面
⊥平面 ,又由(1)知
,又由(1)知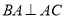 ,
,
建立如图所示的空间直角坐标系 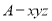 .则
.则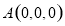 ,
,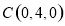 ,
,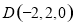 ,
, ,
, ,
,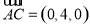
设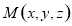 ,
,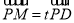 ,则
,则 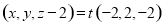 ,
,
故点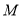 坐标为
坐标为 ,
,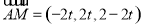 8分
8分
设平面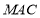 的法向量为
的法向量为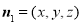 ,则
,则 9分
9分
所以
令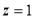 ,则
,则 . 10分
. 10分
又平面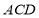 的法向量
的法向量
所以 , 解得
, 解得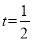
故点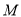 为线段
为线段 的中点. 12分
的中点. 12分
考点:1、直线与平面垂直的判定与性质;2、空间直角坐标系;3、空间向量的夹角公式及应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一理科数学试卷(解析版) 题型:解答题
己知函数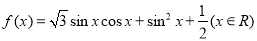
(1)当 时,求函数
时,求函数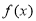 的最小值和最大值;
的最小值和最大值;
(2)设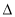 ABC的内角A,B,C的对应边分别为a,b,c,且c=
ABC的内角A,B,C的对应边分别为a,b,c,且c=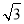 ,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省潍坊市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
某几何体的三视图如图所示,则该几何体外接球的表面积为( )

A.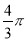 B.
B. C.
C.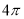 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省潍坊市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
设集合 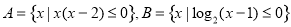 ,则
,则 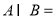 ( )
( )
A.[1,2] B.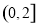 C.(1,2] D.(1,2)
C.(1,2] D.(1,2)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:选择题
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是
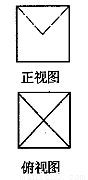
A.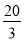 B.6 C.4 D.
B.6 C.4 D.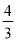
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试文科数学试卷(解析版) 题型:选择题
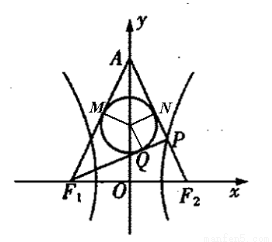
如图,已知双曲线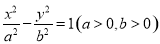 的左、右焦点分别为
的左、右焦点分别为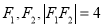 ,P是双曲线右支上的一点,
,P是双曲线右支上的一点,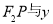 轴交于点A,
轴交于点A,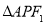 的内切圆在
的内切圆在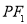 上的切点为Q,若
上的切点为Q,若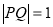 ,则双曲线的离心率是
,则双曲线的离心率是
A.3 B.2 C. D.
D.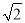
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:填空题
某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分……第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有 名.
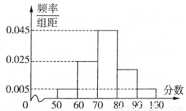
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com