
 ,当θ∈
,当θ∈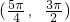 时,f(sin 2θ)-f(-sin 2θ)可化简为
时,f(sin 2θ)-f(-sin 2θ)可化简为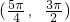 时,利用二倍角公式的应用,以及三角函数在各个象限中的符号,化简f(sin 2θ)=cosθ-sinθ,f(-sin 2θ)=-cosθ-sinθ,从而求得
时,利用二倍角公式的应用,以及三角函数在各个象限中的符号,化简f(sin 2θ)=cosθ-sinθ,f(-sin 2θ)=-cosθ-sinθ,从而求得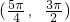 时,f(sin 2θ)=
时,f(sin 2θ)=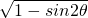 =|cosθ-sinθ|=cosθ-sinθ.
=|cosθ-sinθ|=cosθ-sinθ. =|cosθ+sinθ|=-cosθ-sinθ.
=|cosθ+sinθ|=-cosθ-sinθ.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| |||
| b+2 |
| |||
| a+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| |||
| b+2 |
| |||
| a+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com