
已知等差数列{an}的公差不为零,a1=25,且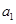 ,
,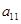 ,
,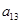 成等比数列.
成等比数列.
(Ⅰ)求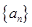 的通项公式;
的通项公式;
(Ⅱ)求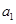 +a4+a7+…+a3n-2.
+a4+a7+…+a3n-2.
(Ⅰ)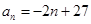 (Ⅱ)
(Ⅱ)
【解析】(Ⅰ)设{an}的公差为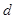 ,由题意,
,由题意,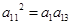 ,
,
即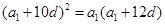 ,于是
,于是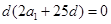 ,又a1=25,所以
,又a1=25,所以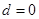 (舍去)或
(舍去)或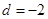 ,
,
故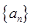 的通项公式为
的通项公式为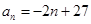 .
.
(Ⅱ)令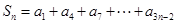 ,则由(Ⅰ)知
,则由(Ⅰ)知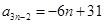 ,故
,故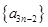 是首项为25,公差为
是首项为25,公差为 的等差数列,从而
的等差数列,从而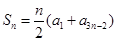 =
=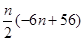 =
= .
.
本题第(Ⅰ)问,由基本量的计算,可以得出公差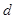 ,从而由等差数列的通项公式求出
,从而由等差数列的通项公式求出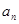 ;第(Ⅱ)问,在等差数列
;第(Ⅱ)问,在等差数列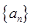 中,每隔两项拿出一项得到的新数列仍成等差数列,公式差为
中,每隔两项拿出一项得到的新数列仍成等差数列,公式差为 ,可以等差数列的前n项和公式求出结果.对第(Ⅰ)问,基本量的计算是高考常考的一个重点内容,注意细心计算确保正确率;准确解答第(Ⅱ)问的关键是熟练等差数列的性质以及前n项和公式.
,可以等差数列的前n项和公式求出结果.对第(Ⅰ)问,基本量的计算是高考常考的一个重点内容,注意细心计算确保正确率;准确解答第(Ⅱ)问的关键是熟练等差数列的性质以及前n项和公式.
【考点定位】本小题主要考查等差数列与等比数列的通项公式与前n项和公式,考查分析问题、解决问题的能力.


科目:高中数学 来源: 题型:
| an | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年周至二中三模理) 已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于 ( )
(A)-4 (B)-6 (C)-8 (D)-10
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三上学期第二次理科数学测试卷(解析版) 题型:选择题
已知等差数列{an}与{bn}的前n项和分别为Sn与Tn, 若 , 则
, 则
 的值是
的值是
A.  B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com