
已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
解 (1)法一 当a=1时,
l1:x+2y+6=0,
l2:x=0,l1不平行于l2;
当a=0时,l1:y=-3,
l2:x-y-1=0,l1不平行于l2;
当a≠1且a≠0时,两直线可化为
l1:y=-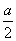 x-3,l2:y=
x-3,l2:y=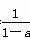 x-(a+1),
x-(a+1),
l1∥l2⇔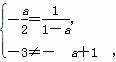 解得a=-1,
解得a=-1,
综上可知,a=-1时,l1∥l2,否则l1与l2不平行.
法二 由A1B2-A2B1=0,得a(a-1)-1×2=0,由A1C2-A2C1≠0,得a(a2-1)-1×6≠0,
∴l1∥l2⇔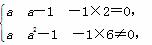
⇔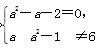 ⇒a=-1,
⇒a=-1,
故当a=-1时,l1∥l2,否则l1与l2不平行.
(2)法一 当a=1时,l1:x+2y+6=0,l2:x=0,l1与l2不垂直,故a=1不成立;
当a=0时,l1:y=-3,l2:x-y-1=0,l1不垂直于l2;
当a≠1且a≠0时,
l1:y=-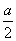 x-3,l2:y=
x-3,l2:y=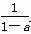 x-(a+1),
x-(a+1),
由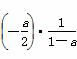 =-1⇒a=
=-1⇒a=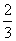 .
.
法二 由A1A2+B1B2=0得a+2(a-1)=0⇒a=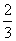 .
.


科目:高中数学 来源: 题型:
(1)已知直线l过点P(3,4)且与点A(-2,2),B(4,-2)等距离,则直线l的方程为( ).
A.2x+3y-18=0
B.2x-y-2=0
C.3x-2y+18=0或x+2y+2=0
D.2x+3y-18=0或2x-y-2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知P是直线l:3x-4y+11=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的两条切线,C是圆心,那么四边形PACB面积的最小值是 ( ).
A.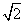 B.2
B.2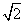 C.
C. D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点P(x0,y0),圆O:x2+y2=r2(r>0),直线l:x0x+y0y=r2,有以下几个结论:①若点P在圆O上,则直线l与圆O相切;②若点P在圆O外,则直线l与圆O相离;③若点P在圆O内,则直线l与圆O相交;④无论点P在何处,直线l与圆O恒相切,其中正确的个数是( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com