练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若A、B是锐角△ABC的两个内角，则点P（cosB－sinA，sinB－cosA）在（   ）

    A．第一象限        B．第二象限        C．第三象限        D．第四象限

     

    【答案】

    B

    【解析】

    试题分析：由题意知A、B、C是锐角，推出A、B的关系，分别求它的正弦和余弦，即可得到结果．解：在锐角三角形ABC中，有A＜90°，B＜90°，C＜90°，又因为A+B+C=180°所以有A+B＞90°，所以有A＞90°-B．又因为Y=cosx在0°＜x＜90°上单调减即cosx的值随x的增加而减少,所以有cosA＜cos（90°-B）=sinB，即cosA＜sinB，sinB-cosA＞0,同理B＞90°-A，则cosB＜cos（90°-A）=sinA，所以cosB-sinA＜0,故答案为B

    考点：三角形内角

    点评：本题考查三角形内角，象限角等知识，是中档题．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若A，B是平面内的两个定点，点P为该平面内动点，且满足向量
    AB
    与
    AP
    夹角为锐角θ，|
    PB
    ||
    AB
    |+
    PA
    •
    AB
    =0    ，则点P的轨迹是（　　）
    A、直线（除去与直线AB的交点）
    B、圆（除去与直线AB的交点）
    C、椭圆（除去与直线AB的交点）
    D、抛物线（除去与直线AB的交点）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中三个内角 A、B、C所对的边分别为a，b，c则下列判断错误的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年北京市东城区东直门中学高三数学提高测试试卷4（理科）（解析版） 题型：选择题

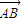    若A，B是平面内的两个定点，点P为该平面内动点，且满足向量与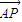夹角为锐角θ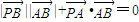，，则点P的轨迹是（ ）
    A．直线（除去与直线AB的交点）
    B．圆（除去与直线AB的交点）
    C．椭圆（除去与直线AB的交点）
    D．抛物线（除去与直线AB的交点）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河南省豫南九校高三第四次联考数学试卷（理科）（解析版） 题型：选择题

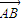    若A，B是平面内的两个定点，点P为该平面内动点，且满足向量与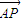夹角为锐角θ，，则点P的轨迹是（ ）
    A．直线（除去与直线AB的交点）
    B．圆（除去与直线AB的交点）
    C．椭圆（除去与直线AB的交点）
    D．抛物线（除去与直线AB的交点）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河南省豫南九校高三第四次联考数学试卷（文科）（解析版） 题型：选择题

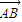    若A，B是平面内的两个定点，点P为该平面内动点，且满足向量与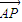夹角为锐角θ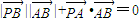，，则点P的轨迹是（ ）
    A．直线（除去与直线AB的交点）
    B．圆（除去与直线AB的交点）
    C．椭圆（除去与直线AB的交点）
    D．抛物线（除去与直线AB的交点）

    查看答案和解析>>

    同步练习册答案