Question

下图所示树形图形中.第一层是一与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与该段均成135°的线段，长度为其一半；第三层按第二层的方法在每一线段的前端生成两条线段；重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.

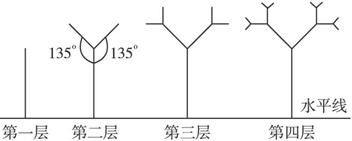
(1)求第三层及第四层树形图的高度H₃，H₄；

(2)求第n层树形图的高度H_n；

(3)若树形图的高度大于2，则称树形图为“高大”，否则称为“矮小”.显然，当n=1,2时是“矮小”的，是否存在m∈Z,使得当n＞m时，该树形图是“高大”的?

Answer 1

思路解析：首先转化成数学模型树（从下而上）,新生的各层高度所构成的数列为{a_n}，然后归纳出第n层树形图的高度，由定义，此树形图永远是“矮小”的.

解：(1)设题中树（从下而上）新生的各层高度所构成的数列为{a_n}，则a₁=1,a₂=×,a₃=,a₄=×，

    所以，第三层树形图的高度H₃=a₁+a₂+a₃=.

    第四层树形图的高度H₄=a₁+a₂+a₃+a₄=.

（2）易知=，所以第n层新生的高度为

    所以当n为奇数时，第n层树形图的高度为

H_n=+=［1-()ⁿ⁺¹］+［1-()^n-1］；

    当n为偶数时，第n层树形图的高度为

H_n=+=［1-()ⁿ］+［1-()ⁿ］.

(3)不存在.

    由（2）知，当n为奇数时，H_n＜{［1-()ⁿ⁺¹］+［1-()^n-1］}=+＜2；

当n为偶数时，H_n＜{［1-()ⁿ］+［1-()ⁿ］}=+＜2，

    由定义，此树形图永远是“矮小”的.所以不存在m∈Z,使得当n＞m时，该树形图是“高大”的.