
【题目】已知圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() .若直线
.若直线![]() 与圆C相交于不同的两点P,Q.
与圆C相交于不同的两点P,Q.
(Ⅰ)写出圆C的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长|PQ|=4,求直线![]() 的斜率.
的斜率.
【答案】(1)(x﹣2)2+(y+3)2=13,圆心为(2,﹣3),半径为![]() (2)0或
(2)0或![]()
【解析】试题分析:(Ⅰ)两边同乘以![]() 利用
利用![]() 可写出圆
可写出圆![]() 的直角坐标方程,并求出圆心的坐标与半径;(Ⅱ)将直线参数方程和的直线过定点根据点斜式可得直线方程为
的直角坐标方程,并求出圆心的坐标与半径;(Ⅱ)将直线参数方程和的直线过定点根据点斜式可得直线方程为![]() ,代入圆的直角坐标方程,根据弦长
,代入圆的直角坐标方程,根据弦长![]() 以及点到直线的距离公式可得以
以及点到直线的距离公式可得以![]() ,从而可求直线
,从而可求直线![]() 的斜率.
的斜率.
试题解析:
解:(Ⅰ)由![]() ,得圆C直角坐标方程x2+y2﹣4x+6y=0,配方,得(x﹣2)2+(y+3)2=13,所以圆心为(2,﹣3),半径为
,得圆C直角坐标方程x2+y2﹣4x+6y=0,配方,得(x﹣2)2+(y+3)2=13,所以圆心为(2,﹣3),半径为![]()
(Ⅱ)由直线![]() 的参数方程知直线过定点M(4,0),则由题意,知直线l的斜率一定存在,
的参数方程知直线过定点M(4,0),则由题意,知直线l的斜率一定存在,
设直线![]() 的方程为y=k(x﹣4),因为弦长|PQ|=4,所以
的方程为y=k(x﹣4),因为弦长|PQ|=4,所以![]() =3,
=3,
解得k=0或k=﹣![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 为奇函数.
为奇函数.
(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ-![]() )=
)=![]() .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试求下列函数的定义域与值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沪昆高速铁路全线2016年12月28日开通运营.途经鹰潭北站的![]() 、
、![]() 两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
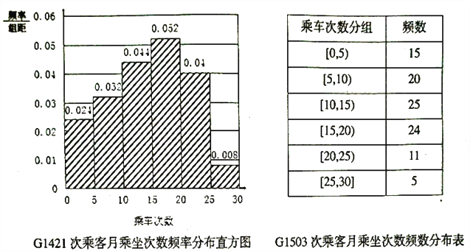
(1)若将频率视为概率,月乘车次数不低于15次的称之为“老乘客”,试问:哪一车次的“老乘客”较多,简要说明理由;
(2)已知在![]() 次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成
次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成![]() 列联表,并根据资料判断,是否有
列联表,并根据资料判断,是否有![]() 的把握认为年龄与乘车次数有关,说明理由.
的把握认为年龄与乘车次数有关,说明理由.
老乘客 | 新乘客 | 合计 | |
50岁以上 | |||
50岁以下 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x![]() (m∈N*).
(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2, ![]() ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且
上的奇函数,且![]() 若对于任意的
若对于任意的![]() 有
有![]()
(1)判断并证明函数的单调性;
(2)解不等式![]() ;
;
(3)若![]() 对于任意的
对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线L的参数方程为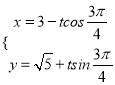 (
(![]() 为参数).在以原点
为参数).在以原点 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标中,圆C的方程为
轴正半轴为极轴的极坐标中,圆C的方程为![]() .
.
(Ⅰ)写出直线L的倾斜角![]() 和圆C的直角坐标方程;
和圆C的直角坐标方程;
(Ⅱ)若点 P坐标为![]() ,圆C与直线L交于 A,B两点,求|PA|
,圆C与直线L交于 A,B两点,求|PA|![]() |PB|的值.
|PB|的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com