
如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,
 点
点![]() ,
,![]() 分别在棱
分别在棱![]() 上,且
上,且![]()
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点![]() 使得二面角
使得二面角![]() 为直二面角?并说明理由.
为直二面角?并说明理由.
解法:本题主要考查直线和平面垂直、直线与平面所成的角、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.
(Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
又![]() ,∴AC⊥BC.
,∴AC⊥BC.
∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,
∴![]() ,
,
又由(Ⅰ)知,BC⊥平面PAC,w.w.w.k.s.5.u.c.o.m ![]()
![]()
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴![]() ,
,
∴在Rt△ABC中,![]() ,∴
,∴![]() .
.
∴在Rt△ADE中,![]() ,
,
∴![]() 与平面
与平面![]() 所成的角的大小
所成的角的大小![]() .
.
(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE![]() 平面PAC,PE
平面PAC,PE![]() 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角![]() 的平面角,
的平面角,
∵PA⊥底面ABC,∴PA⊥AC,∴![]() .
.
∴在棱PC上存在一点E,使得AE⊥PC,这时![]() ,
,
故存在点E使得二面角![]() 是直二面角.
是直二面角.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(本小题共14分)如图,在三棱锥![]() 中,
中,![]() 底面
底面
![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() 上,且
上,且![]() (Ⅰ)求证:
(Ⅰ)求证:![]() 平面
平面![]() ;(Ⅱ)当
;(Ⅱ)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成的角的大小;(Ⅲ)是否存在点
所成的角的大小;(Ⅲ)是否存在点![]() 使得二面角
使得二面角![]() 为直二面角?并说明理由.
为直二面角?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分10分)
如图,在三棱锥 中,
中,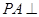 底面
底面 ,
点
,
点 ,
,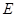 分别在棱
分别在棱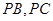 上,且
上,且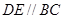

(Ⅰ)求证: 平面
平面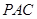 ;
;
(Ⅱ)当 为
为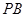 的中点时,求
的中点时,求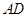 与平面
与平面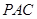 所成的角的正弦值;
所成的角的正弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com