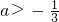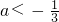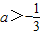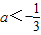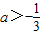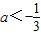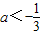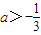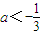若函数y=e(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是
- A.
a>-3
- B.
a<-3
- C.
- D.
B
分析:由题意可得:y′=(a-1)e
(a-1)x+4(a<1),即可得到函数的零点为x
0=
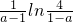
,所以x
0=
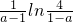
>0,进而求出a的范围.
解答:因为函数y=e
(a-1)x+4x,
所以y′=(a-1)e
(a-1)x+4(a<1),
所以函数的零点为x
0=
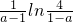
,
因为函数y=e
(a-1)x+4x(x∈R)有大于零的极值点,
所以x
0=
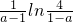
>0,即
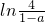
<0,
解得:a<-3.
故选B.
点评:本题主要考查利用导数求函数的极值点,以及对数函数的单调性等知识点,此题属于基础题.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
(2010•深圳模拟)若函数y=e(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省聊城市高三(上)第一次调研数学试卷(理科)(解析版)
题型:选择题
若函数y=e
(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是( )
A.a>-3
B.a<-3
C.
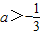
D.
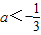
查看答案和解析>>
科目:高中数学
来源:2012-2013学年新疆乌鲁木齐一中高三(上)第一次月考数学试卷(理科)(解析版)
题型:选择题
若函数y=e
(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是( )
A.a>-3
B.a<-3
C.
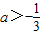
D.
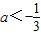
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省聊城市高三(上)第一次调研数学试卷(理科)(解析版)
题型:选择题
若函数y=e
(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是( )
A.a>-3
B.a<-3
C.

D.
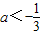
查看答案和解析>>
科目:高中数学
来源:2009-2010学年广东省深圳市五校高三联考数学试卷(理科)(解析版)
题型:选择题
若函数y=e
(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是( )
A.a>-3
B.a<-3
C.
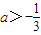
D.
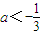
查看答案和解析>>