
分析 (Ⅰ)m=1时,f(x)=lnx+$\frac{1}{x}$,利用f′(x)判定f(x)的增减性并求出f(x)的极小值;
(Ⅱ)由函数g(x)=f′(x)-$\frac{x}{3}$,令g(x)=0,求出m;设φ(x)=m,求出φ(x)的值域,讨论m的取值,对应g(x)的零点情况;
(Ⅲ)求出h(x)的导数,问题转化为m≥x-x2在(0,+∞)恒成立,根据二次函数的性质求出m的范围即可.
解答 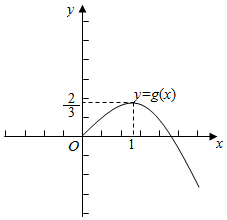 解:(Ⅰ)当m=1时,f(x)=lnx+$\frac{1}{x}$,
解:(Ⅰ)当m=1时,f(x)=lnx+$\frac{1}{x}$,
∴f′(x)=$\frac{x-1}{{x}^{2}}$;
∴当x∈(0,1)时,f′(x)<0,f(x)在(0,1)上是减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上是增函数;
∴x=1时,f(x)取得极小值为f(1)=ln1+1=1;
(Ⅱ)∵函数g(x)=f′(x)-$\frac{x}{3}$=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$-$\frac{x}{3}$(x>0),
令g(x)=0,得m=-$\frac{1}{3}$x3+x(x>0);
设φ(x)=-$\frac{1}{3}$x3+x(x>0),
∴φ′(x)=-x2+1=-(x-1)(x+1);
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上是增函数,
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上是减函数;
∴x=1是φ(x)的极值点,且是极大值点,
∴x=1是φ(x)的最大值点,
∴φ(x)的最大值为φ(1)=$\frac{2}{3}$;
又φ(0)=0,结合y=φ(x)的图象,如图;
当0<m<$\frac{2}{3}$时,函数g(x)有两个零点;
(Ⅲ)h(x)=lnx+$\frac{m}{x}$-x,(x>0),
h′(x)=$\frac{x-m{-x}^{2}}{{x}^{2}}$,
若h(x)在(0,+∞)上单调递减,
则x-m-x2≤0在(0,+∞)恒成立,
即m≥x-x2在(0,+∞)恒成立,
而y=x-x2在(0,+∞)的最大值是$\frac{1}{4}$,
∴m≥$\frac{1}{4}$.
点评 本题考查了导数的综合应用问题,解题时应根据函数的导数判定函数的增减性以及求函数的极值和最值,应用分类讨论法,构造函数等方法来解答问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:解答题
如图,四边形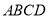 为梯形,
为梯形, ,
,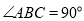 ,求图中阴影部分绕
,求图中阴影部分绕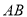 旋转一周形成的几何体的表面积和体积.
旋转一周形成的几何体的表面积和体积.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
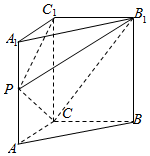 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
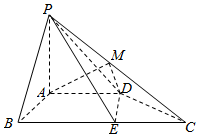 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD,BC=4,点M为PC中点,点E为BC边上的动点,且$\frac{BE}{EC}=λ$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD,BC=4,点M为PC中点,点E为BC边上的动点,且$\frac{BE}{EC}=λ$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
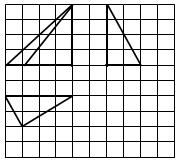 如图:网格上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面面积中的最大值为( )
如图:网格上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面面积中的最大值为( )| A. | 16 | B. | 8 | C. | 2$\sqrt{13}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
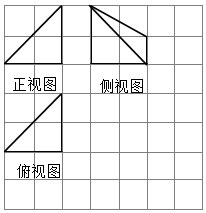 某几何体的三视图如图所示,图中小方格的长度为1,则该几何体的体积为( )
某几何体的三视图如图所示,图中小方格的长度为1,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | 2 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
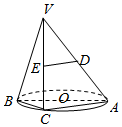 AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com