
已知函数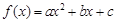 ,
,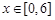 的图象经过
的图象经过 和
和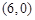 两点,如图所示,且函数
两点,如图所示,且函数 的值域为
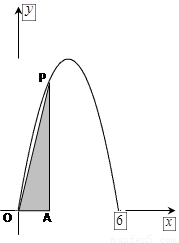
的值域为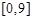 .过该函数图象上的动点
.过该函数图象上的动点 作
作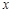 轴的垂线,垂足为
轴的垂线,垂足为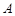 ,连接
,连接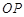 .
.
(I)求函数 的解析式;
的解析式;
(Ⅱ)记 的面积为
的面积为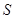 ,求
,求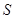 的最大值.
的最大值.
(I)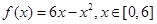 ;(II)三角形面积的最大值为16.
;(II)三角形面积的最大值为16.
【解析】
试题分析:(I)用待定系数法.由抛物线的对称性及题设可知,函数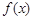 的对称轴为
的对称轴为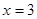 ,顶点为
,顶点为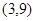 .
.
将顶点坐标及点(0,0),(0,6)的坐标代入解析式得关于a,b,c方程组,解此方程组,便可得 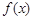 的解析式.
的解析式.
(II)用三角形面积公式求得三角形的面积与t之间的函数关系式,然后利用导数可求得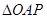 的面积为
的面积为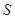 ,求
,求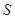 的最大值.
的最大值.
试题解析:(I)由已知可得函数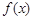 的对称轴为
的对称轴为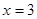 ,顶点为
,顶点为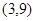 .
2分
.
2分
方法一:由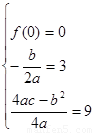
得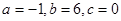 5分
5分
得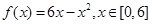 6分
6分
方法二:设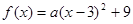 4分
4分
由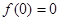 ,得
,得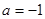 5分
5分
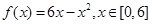 6分
6分
(II)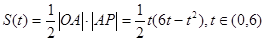 8分
8分
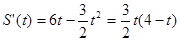 9分
9分
列表得:
|
|
|
4 |
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
11分
由上表可得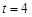 时,三角形面积取得最大值
时,三角形面积取得最大值
即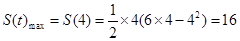 13分
13分
考点:1、二次函数;2、导数


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2012-2013学年江西省九江市都昌二中高三(上)第四次月考数学试卷(文科)(解析版) 题型:填空题
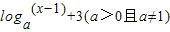 的图象恒过点P,若角α的终边经过点P,则cos2α-sin2α的值等于 .
的图象恒过点P,若角α的终边经过点P,则cos2α-sin2α的值等于 .查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,
,![]() 的图象经过
的图象经过![]() 和
和![]() 两点,如图所示,且函数
两点,如图所示,且函数![]() 的值域为
的值域为![]() .过该函数图象上的动点
.过该函数图象上的动点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .(I)求函数
.(I)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com