
已知公比为![]() 的等比数列{
的等比数列{![]() }是递减数列,且满足
}是递减数列,且满足![]() +
+![]() +
+![]() =
=![]() ,
,![]()
![]()
![]() =
=![]()
(I)求数列{![]() }的通项公式;
}的通项公式;
(II)求数列{![]() }的前
}的前![]() 项和为
项和为![]() ;
;
(Ⅲ)若![]() ,证明:
,证明:![]() ≥
≥![]() .
.
解:由![]()
![]()
![]() =
=![]() ,及等比数列性质得
,及等比数列性质得![]() =
=![]() ,即
,即![]() =
=![]() ,……1分
,……1分
由![]() +
+![]() +
+![]() =
=![]() 得
得![]() +
+![]() =
=![]()
由 得
得 所以
所以![]() ,即3
,即3![]() 2-10
2-10![]() +3=0
+3=0
解得![]() =3,或
=3,或![]() =
=![]() …………………………3分
…………………………3分
因为{![]() }是递减数列,故
}是递减数列,故![]() =3舍去,∴
=3舍去,∴![]() =
=![]() ,由
,由![]() =
=![]() ,得
,得![]() =1
=1
故数列{![]() }的通项公式为
}的通项公式为![]() =
=![]() (
(![]() ∈N*)………………4分
∈N*)………………4分
(II)由(I)知![]() =
=![]() ,所以
,所以![]() =1+
=1+![]() +
+![]() +…+
+…+![]() ①
①
![]()
![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]() +
+![]() ②……………………5分
②……………………5分
①-② 得:![]()
![]() =1+
=1+![]() +
+![]() +
+![]() +…+
+…+![]() -
-![]()
=1+2(![]() +
+![]() +
+![]() +…+
+…+![]() )-
)-![]()
=1+2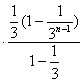 -
-![]() =2-
=2-![]() -
-![]()
所以![]() =3-
=3-![]() ………………………………8分
………………………………8分
(Ⅲ)因为![]() =
=![]() +
+![]() =
=![]() ,……………………9分
,……………………9分
所以![]() =
=![]() +
+![]() +…+
+…+![]()
=2[(![]() )+(
)+(![]() )+…+(
)+…+(![]() )]
)]
=2(![]() -
-![]() )……………………11分
)……………………11分
因为![]() ≥1,
≥1,![]() -
-![]() ≥
≥![]() =
=![]() ,
,
所以![]() ≥
≥![]() .…………………………12分
.…………………………12分


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源:2013-2014学年上海市高三八校联合调研考试文科数学试卷(解析版) 题型:选择题
已知公比为 的等比数列
的等比数列 的前
的前 项和为
项和为 ,则下列结论中:
,则下列结论中:
(1) 成等比数列;
成等比数列;
(2) ;
;
(3)
正确的结论为 ( )
(A)(1)(2). (B)(1)(3). (C)(2)(3). (D)(1)(2)(3).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷(二)(解析版) 题型:解答题
各项均为正数的数列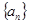 前
前 项和为
项和为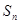 ,且
,且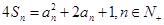 .
.
(1)求数列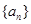 的通项公式;
的通项公式;
(2)已知公比为 的等比数列
的等比数列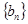 满足
满足 ,且存在
,且存在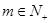 满足
满足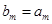 ,
,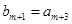 ,求数列
,求数列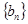 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修五2.5等比数列前n项和练习卷(解析版) 题型:选择题
已知公比为
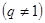 的等比数列
的等比数列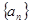 的前
的前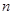 项和为
项和为 ,
,
则数列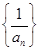 的前
的前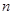 项和为 (
)
项和为 (
)
A.  B.
B.
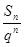 C.
C.
 D.
D.
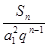
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com