
【题目】已知函数f(x)=loga(x﹣1),g(x)=loga(6﹣2x)(a>0且a≠1).
(1)求函数φ(x)=f(x)+g(x)的定义域;
(2)试确定不等式f(x)≤g(x)中x的取值范围.
【答案】
(1)解:由 ![]() ,解得1<x<3.
,解得1<x<3.
∴函数(x)的定义域为{x|1<x<3}
(2)解:不等式f(x)≤g(x),即为loga(x﹣1)≤loga(6﹣2x),
②当a>1时,不等式等价于 ![]() ,解得:
,解得: ![]() ;
;
②当0<a<1时,不等式等价于 ![]() ,解得:
,解得: ![]() .
.
综上可得,当a>1时,不等式的解集为(1, ![]() ];
];
当0<a<1,不等式的解集为[ ![]() )
)
【解析】(1)直接由对数式的真数大于0联立不等式组求解x的取值集合得答案;(2)分a>1和0<a<1求解不等式得答案.
【考点精析】本题主要考查了函数的定义域及其求法和指、对数不等式的解法的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;指数不等式的解法规律:根据指数函数的性质转化;对数不等式的解法规律:根据对数函数的性质转化才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;指数不等式的解法规律:根据指数函数的性质转化;对数不等式的解法规律:根据对数函数的性质转化才能正确解答此题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】对于数列{an},定义 ![]() 为{an}的“优值”,现在已知某数列{an}的“优值”
为{an}的“优值”,现在已知某数列{an}的“优值” ![]() ,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg( ![]() )为奇函数.
)为奇函数.
(1)求m的值,并求f(x)的定义域;
(2)判断函数f(x)的单调性,并证明;
(3)若对于任意θ∈[0, ![]() ],是否存在实数λ,使得不等式f(cos2θ+λsinθ﹣
],是否存在实数λ,使得不等式f(cos2θ+λsinθ﹣ ![]() )﹣lg3>0.若存在,求出实数λ的取值范围;若不存在,请说明理由.
)﹣lg3>0.若存在,求出实数λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex+ax2+2x+1在x=﹣1处取得极值.
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)﹣m﹣1在[﹣2,2]上恰有两个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图. 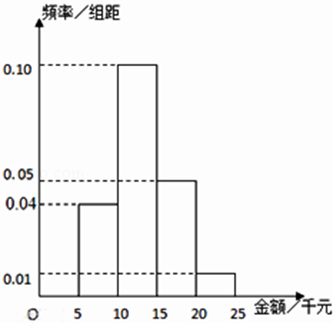
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足 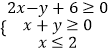 ,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
A.[﹣1,2]
B.[﹣2,1]
C.[2,3]
D.[﹣1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在自然数列1,2,3,,n中,任取k个元素位置保持不动,将其余n﹣k个元素变动位置,得到不同的新数列.由此产生的不同新数列的个数记为Pn(k).
(1)求P3(1)
(2)求 ![]() P4(k);
P4(k);
(3)证明 ![]() kPn(k)=n
kPn(k)=n ![]() Pn﹣1(k),并求出
Pn﹣1(k),并求出 ![]() kPn(k)的值.
kPn(k)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com