


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
某造船公司年造船量是20艘,已知造船![]() 艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。
艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。
(Ⅰ)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数MP(x)单调递减时x的取值范围,并说明单调递减在本题中的实际意义是什么?查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省四地六校高二下学期第一次月考数学理卷 题型:解答题
((本小题12分)某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为
 (单位:万元),成本函数为
(单位:万元),成本函数为 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数 的边际函数
的边际函数 定义为
定义为 。
。
(Ⅰ)求利润函数 及边际利润函数
及边际利润函数 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数 单调递减时
单调递减时 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011年新疆农七七师高级中学高二下学期第一学段考试理科数学 题型:解答题
(本小题12分)
某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为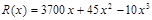 (单位:万元),成本函数为
(单位:万元),成本函数为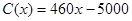 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数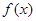 的边际函数
的边际函数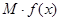 定义为
定义为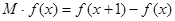 。
。
(Ⅰ)求利润函数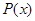 及边际利润函数
及边际利润函数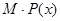 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数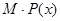 单调递减时
单调递减时 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com