
 ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为 假定汽车只在遇到红灯或到达目的地才停止前进,
假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求: 的概率的分布列及期望E
的概率的分布列及期望E ;
;科目:高中数学 来源:不详 题型:解答题
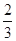 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙答对每个题的概率为
,乙答对每个题的概率为 。
。 ,求
,求 的分布列和数学期望;
的分布列和数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
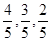 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com