练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    不等式ex－x>ax的解集为P，且[0,2]⊆P，则实数a的取值范围是(　　)

    A．(－∞，e－1)  B．(e－1，＋∞)C．(－∞，e＋1)  D．(e＋1，＋∞)

     

    【答案】

    A

    【解析】因为ex－x>ax的解集为P，且[0,2]⊆P，所以对任意x∈[0,2]，ex－x>ax恒成立，当x＝0时，不等式成立，故0<x≤2时，a<－1恒成立．

     

    令g(x)＝－1，则g′(x)＝，当1<x≤2时，g′(x)>0，当0<x<1时，g′(x)<0.

     

    所以当x＝1时，g(x)取得最小值e－1，所以a的取值范围是(－∞，e－1)，故选A.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013年湖北新洲、红安、麻城一中高三上学期期末考文科数学试卷（解析版） 题型：解答题

     (本小题满分14分)

    已知函数f (x)=ex，g(x)=lnx，h(x)=kx+b.

    (1)当b=0时，若对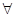x∈（0，+∞）均有f (x)≥h(x)≥g(x)成立，求实数k的取值范围；

    (2)设h(x)的图象为函数f (x)和g(x)图象的公共切线，切点分别为(x1, f (x1))和(x2, g(x2))，其中x1>0.

    ①求证：x1>1>x2；

    ②若当x≥x1时，关于x的不等式ax2－x+xe+1≤0恒成立，求实数a的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：辽宁省模拟题 题型：解答题

    已知函数f（x）=ex-x（e为自然对数的 底数）。
    （1）求f（x）的最小值；
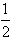    （2）不等式f（x）>ax的解集为P，若M={x|≤x≤2}且M∩P≠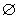，求实数a的取值范围；
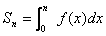    （3）已知n∈N*，且，是否存在等差数列{an} 和首项为f（1），公比大于0的等比数列{bn}，使得a1+a2+…+an+b1+b2+…+bn=Sn？若存在，请求出数列{an}、{bn}的通项公式；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=ln(ex+a)(a>0)   (1)求函数y=f(x)的反函数y=f-1(x)及f(x)的导数f′(x)． (2)假设对任意x∈[ln(3a)，ln(4a)]．不等式｜m-f-1(x)｜lnf′(x)<0成立．求实数m的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

     （10分）要求考生从下面两个题中任选一题，多选者按第一选项给分。

      （1）求证：当x>－1时，不等式ln(x+1)<x+1≤ex成立。

                                                              

                                                              

      （2）求函数f(x)=ex(1－x2)的单调递增区间。

                                                              

                                                              

    查看答案和解析>>

    同步练习册答案