分析:(I)由题设知a
1=1,a
n=S
n-S
n-1=
(an2+an)-(an-12+an-1),a
n2-a
n-12-a
n-a
n-1=0,故(a
n+a
n-1)(a
n-a
n-1-1)=0,由此能导出a
n=n.于是b
n+1=b
n+3
n,b
n+1-b
n=3
n,由此能求出b
n.
(II)
cn=n•3n,
Tn=(1×3+2×32+…n×3n),由错位相减法能求出
Tn =,由此能得到
==
=
(-+• )=.
解答:解:(I)
a1 =S1=(a12+a1),∴a
1=1,
n≥2时,a
n=S
n-S
n-1=
(an2+an)-(an-12+an-1),
∴a
n2-a
n-12-a
n-a
n-1=0,
(a
n+a
n-1)(a
n-a
n-1-1)=0,
∴a
n-a
n-1=1.
∴数列{a
n}是首项为1,公差为1的等差数列,
∴a
n=n.
于是b
n+1=b
n+3
n,∴b
n+1-b
n=3
n,b
n=b
1+(b
2-b
1)+(b
3-b
2)+…+(b
n-b
n-1)
=
+3+32+…+3n-1=+=.
(II)
cn=n•3n,
∴
Tn=(1×3+2×32+…n×3n),
3Tn=(1×32+2×33+…+n×3n+1),
∴
2Tn=(n•3n+1-3-32-…-3n)=
(n•3n+1-)=
,
Tn =,
∴
==
=
(-+• )=.
点评:第(I)题考查数列通项公式的求法,解题时要注意迭代法的合理运用;第(II)题考查前n项和的计算和极限在数列中的运用,解题时要认真审题,仔细解答,注意数列性质的合理运用.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案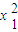 +
+ +…+
+…+ ,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;
,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B; +
+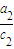 +
+ 的最小值为3;
的最小值为3; +
+ +…+
+…+ +
+ 的最小值为
的最小值为 .
.