
【题目】在平面直角坐标系中,直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12. (Ⅰ)写出直线l的极坐标方程与曲线C的直角坐标方程;
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12. (Ⅰ)写出直线l的极坐标方程与曲线C的直角坐标方程;
(Ⅱ)已知与直线l平行的直线l'过点M(1,0),且与曲线C交于A,B两点,试求|AB|.
【答案】解:(Ⅰ)直线l的直角坐标方程为 ![]() , 所以直线l的极坐标方程为
, 所以直线l的极坐标方程为 ![]()
又因为曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12,
所以曲线C的直角坐标方程为3x2+4y2=12,化简得 ![]() .
.
(Ⅱ)因为直线l'与直线l平行,
又M(1,0)在直线l'上,∴直线l'的参数方程为  ,(t为参数),
,(t为参数),
将它代入曲线C的方程中得 ![]() ,
,
所以 ![]() .
.
【解析】(Ⅰ)先求出直线l的直角坐标方程,由此能求出直线l的极坐标方程;由曲线C的极坐标方程,能求出曲线C的直角坐标方程.(Ⅱ)由直线l'与直线l平行,M(1,0)在直线l'上,能求出直线l'的参数方程,将它代入曲线C的方程得 ![]() ,由此能求出|AB|.
,由此能求出|AB|.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足(p﹣1)Sn=p2﹣an(p>0,p≠1),且a3= ![]() .
.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bnbn+2}的前n项和为Tn , 若对于任意的正整数n,都有Tn<m2﹣m+
,数列{bnbn+2}的前n项和为Tn , 若对于任意的正整数n,都有Tn<m2﹣m+ ![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)设该公司从至少消费两次,求这的顾客消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出2人中恰有1人消费两次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,点
,点![]() 是坐标平面内一点,且
是坐标平面内一点,且![]() ,
, ![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的动直线
的动直线![]() 交椭圆于
交椭圆于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使以
,使以![]() 为直径的圆恒过该点?若存在,求出点
为直径的圆恒过该点?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线C: ![]() =1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=
=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ= ![]() ,且
,且 ![]() |,则双曲线C的离心率为( )
|,则双曲线C的离心率为( ) 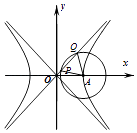
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx(x>0)的图象与x轴相切于点(3,0). (Ⅰ)求函数f(x)的解析式;
(Ⅱ)若g(x)+f(x)=﹣6x2+(3c+9)x,命题p:x1 , x2∈[﹣1,1],|g(x1)﹣g(x2)|>1为假命题,求实数c的取值范围;
(Ⅲ)若h(x)+f(x)=x3﹣7x2+9x+clnx(c是与x无关的负数),判断函数h(x)有几个不同的零点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列共有四个命题: ⑴命题“ ![]() ”的否定是“x∈R,x2+1<3x”;
”的否定是“x∈R,x2+1<3x”;
⑵在回归分析中,相关指数R2为0.96的模型比R2为0.84的模型拟合效果好;
⑶a,b∈R, ![]() ,则p是q的充分不必要条件;
,则p是q的充分不必要条件;
⑷已知幂函数f(x)=(m2﹣3m+3)xm为偶函数,则f(﹣2)=4.
其中正确的序号为 . (写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com