
分析 (1)由g($\frac{1}{2}$)=$\sqrt{2}$,可得y=g(x)的解析式;由函数f(x)=$\frac{1-g(x)}{m+2g(x)}$是奇函数,可得m值,进而可得y=f(x)解析式;
(2)函数f(x)在R为减函数,作差判断可得绪论;
(3)f(x)在(-∞,+∞)上为减函数.又因为f(x)是奇函数,所以不等式f(t2-2t)+f(2t2-1)<0等价于t2-2t>-2t2+1,解得答案.
解答 解:(1)设g(x)=ax,
∴g($\frac{1}{2}$)=${a}^{\frac{1}{2}}$=$\sqrt{2}$,
∴a=2,
∴g(x)=2x,
∴f(x)=$\frac{1-{2}^{x}}{m+2•{2}^{x}}$,
∵f(x)是奇函数,
∴f(-x)=-f(x),
即$\frac{1-{2}^{-x}}{m+2•{2}^{-x}}$=$\frac{{2}^{x}-1}{m{2}^{x}+2}$=-$\frac{1-{2}^{x}}{m+2•{2}^{x}}$,
解得m=2,
∴f(x)=$\frac{1-{2}^{x}}{2+2•{2}^{x}}$ (4分)
(2)函数f(x)在R为减函数,理由如下:
任取x1,x2∈R,且x1<x2,
则$1+{2}^{{x}_{1}}>0$,$1+{2}^{{x}_{2}}>0$,${{2}^{{x}_{2}}-2}^{{x}_{1}}>0$
∴f(x1)-f(x2)=$\frac{1-{2}^{{x}_{1}}}{2+2•{2}^{{x}_{1}}}$-$\frac{1-{2}^{{x}_{2}}}{2+2•{2}^{{x}_{2}}}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$>0,
即f(x1)>f(x2)…(6分)
故函数f(x)在R为减函数. (8分)
(3)f(x)在(-∞,+∞)上为减函数.又因为f(x)是奇函数,
所以不等式f(t2-2t)+f(2t2-1)<0等价于f(t2-2t)<-f(2t2-1)=f(-2t2+1).
因为f(x)是减函数,由上式推得t2-2t>-2t2+1,即3t2-2t-1>0,
解不等式可得{t|t>1或$\left.{t<-\frac{1}{3}}\right\}$.(12分)
点评 本题考查的知识点是函数的奇偶性,函数的单调性,转化思想,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | [1,2] | C. | (1,2] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
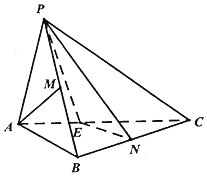 如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com