
 ,
, ,则tanα=________.
,则tanα=________.
 两边平方后,利用同角三角函数间的基本关系求出sinα-cosα=-
两边平方后,利用同角三角函数间的基本关系求出sinα-cosα=- ,两者联立求出sinα和cosα的值,即可得到tanα的值.
,两者联立求出sinα和cosα的值,即可得到tanα的值. >0,两边平方得(sinα+cosα)2=
>0,两边平方得(sinα+cosα)2= ,化简得1+2sinαcosα=
,化简得1+2sinαcosα=
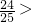 0,
0, ,且
,且  ,
, ,与
,与 ,联立解得sinα=
,联立解得sinα= ,cosα=
,cosα= ,
,



 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com