
(满分15分)设函数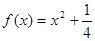 ,
,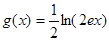 ,(其中
,(其中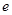 为自然底数);
为自然底数);
(Ⅰ)求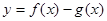 (
(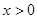 )的最小值;
)的最小值;
(Ⅱ)探究是否存在一次函数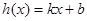 使得
使得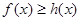 且
且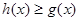 对一切
对一切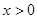 恒成立;若存在,求出一次函数的表达式,若不存在,说明理由;
恒成立;若存在,求出一次函数的表达式,若不存在,说明理由;
(Ⅲ)数列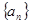 中,
中,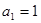 ,
,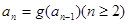 ,求证:
,求证: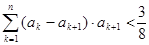 。
。
(Ⅰ)0(Ⅱ)存在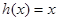 符合要求,理由见解析(Ⅲ)先证
符合要求,理由见解析(Ⅲ)先证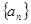 递减且
递减且 ,再利用放缩不等式证明
,再利用放缩不等式证明
【解析】
试题分析:(Ⅰ)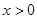 时
时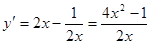 ,
,
易知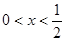 时
时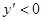 、
、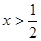 时
时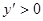 ;
;
所以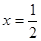 时求
时求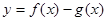 取最小值等于0; ……4分
取最小值等于0; ……4分
(Ⅱ)由题Ⅰ易知,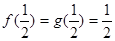 ,所以
,所以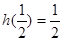 ; ……6分
; ……6分
所以可设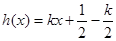 ,代入
,代入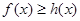
得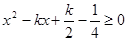 恒成立,所以
恒成立,所以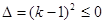 ,
,
所以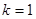 ,
,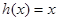 ; ……8分
; ……8分
此时设 ,
,
则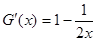 ,易知
,易知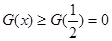 ,即
,即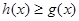 对一切
对一切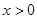 恒成立;
恒成立;
综上,存在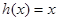 符合要求,它恰好是
符合要求,它恰好是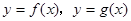 图象的公切线. ……10分
图象的公切线. ……10分
(Ⅲ)先证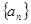 递减且
递减且 ;
;
由题(Ⅱ)知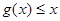 ,所以
,所以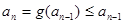 ,即
,即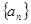 为递减数列;
为递减数列;
又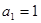 ,
,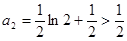 ,所以
,所以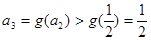 ,…
,…
因为当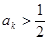 时总有
时总有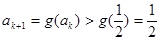 ,
,
所以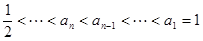 ; ……13分
; ……13分
所以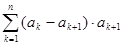
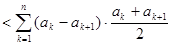
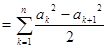
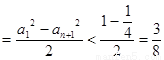 . ……15分
. ……15分
考点:本小题主要考查利用导数求最值、利用导数求解和恒成立问题和利用导数证明不等式,考查学生利用导数这个工具解决问题的能力和运算求解能力.
点评:导数是研究函数的性质如单调性、极值、最值等的有力工具,有时也用导数来解决实际应用题,要注意研究导数性质的时候不要忘记函数的定义域.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com