
由正整数组成的一组数据x1,x2,x3, x4,其平均数和中位数都是2,且标准差等于1,则这组数据为 .(从小到大排列)
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:填空题
若m,n∈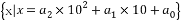 ,其中ai(i=0,1,2)∈
,其中ai(i=0,1,2)∈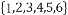 ,并且m+n=606,则实数对(m,n)表示平面上不同点的个数为 .
,并且m+n=606,则实数对(m,n)表示平面上不同点的个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十八第十章第五节练习卷(解析版) 题型:选择题
有5本不同的书,其中语文书2本,数学书2本,物理书1本.若将其随机地并排摆放到图书架的同一层上,则同一科目的书都不相邻的概率是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:选择题
2012年山东文博会期间,某班有甲、乙、丙、丁四名学生参加了志愿者服务工作.将这四名学生分配到A,B,C三个不同的展馆服务,每个展馆至少分配一人.若甲要求不到A馆,则不同的分配方案有( )
(A)36种 (B)30种 (C)24种 (D)20种
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十二第九章第三节练习卷(解析版) 题型:填空题
为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为 (用“>”连接).
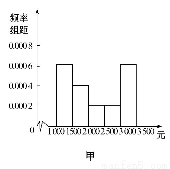
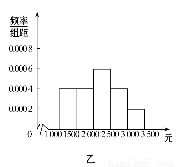
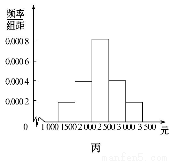
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十二第九章第三节练习卷(解析版) 题型:选择题
为选拔运动员参加比赛,测得7名选手的身高(单位:cm)分布茎叶图为

记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数字记为x,那么x的值为( )
(A)5 (B)6 (C)7 (D)8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十九第十章第六节练习卷(解析版) 题型:解答题
设函数f(x)=x2+bx+c,其中b,c是某范围内的随机数,分别在下列条件下,求事件A“f(1)≤5且f(0)≤3”发生的概率.
(1)若随机数b,c∈{1,2,3,4}.
(2)已知随机函数Rand( )产生的随机数的范围为{x|0≤x≤1},b,c是算法语句b=4*Rand( )和c=4*Rand( )的执行结果.(注:符号“*”表示“乘号”)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
甲、乙两颗卫星同时监测台风,在同一时刻,甲、乙两颗卫星准确预报台风的概率分别为0.8和0.75,则在同一时刻至少有一颗卫星预报准确的概率为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业八十一选修4-5第三节练习卷(解析版) 题型:解答题
已知正数x,y,z满足5x+4y+3z=10.
(1)求证: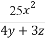 +
+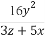 +
+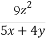 ≥5.
≥5.
(2)求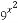 +
+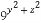 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com