
下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]()
![]() 面
面![]() ;
;
(Ⅱ)证明![]() 面
面![]() ;
;
(Ⅲ)求面![]() 与面
与面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.

解: (Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,
∴PD⊥AF,
又∵CD⊥DA,CD⊥PA,PA∩DA=A,
∴CD⊥面ADP,
∴CD⊥AF.又CD∩DP=D, ∴AF⊥面PC D. ------------- 4分
(Ⅱ)取PC的中点M,AC与BD的交点为N,连结MN,
∴MN=![]() PA,MN∥PA,
PA,MN∥PA,
∴MN=EB,MN∥EB,故四边形BEMN为平行四边形,
∴EM∥BN,又EM![]() 面PEC,∴BD∥面PE C. -------------7分
面PEC,∴BD∥面PE C. -------------7分
(Ⅲ)分别以BC,BA,BE为x,y,z轴建立空间直角坐标系,
则C( 4,0,0),D(4 ,4 , 0),E(0,0,2),A(0,4 ,0),P(0,4,4),
∵F为PD的中点,∴F(2,4,2).
∵AF⊥面PCD,∴![]() 为面PCD的一个法向量,
为面PCD的一个法向量,
![]() =(-2,0,-2),设平面PEC的法向量为
=(-2,0,-2),设平面PEC的法向量为![]() =(x,y ,z),
=(x,y ,z),
则 ,
,
∴![]() ,令x=1,∴
,令x=1,∴![]() , -------------10分
, -------------10分
∴
∴![]() 与
与![]() 的夹角为
的夹角为![]() .
.
面PEC与面PDC所成的二面角(锐角)的余弦值为![]() . -------------12分
. -------------12分


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
 下图是一几何体的直观图、主观图、左视图、俯视图.其中俯视图为正方形,主视图为直角梯形,左视图为等腰直角三角形,且CE是中线.
下图是一几何体的直观图、主观图、左视图、俯视图.其中俯视图为正方形,主视图为直角梯形,左视图为等腰直角三角形,且CE是中线.查看答案和解析>>
科目:高中数学 来源: 题型:
(08年青岛市质检二理) (12分) 下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 面
面![]() ;
;
(Ⅱ)证明:![]() ∥面
∥面![]() ;
;
(Ⅲ)求面![]() 与面
与面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省、楚雄一中、昆明三中高三第二次联考文科数学 题型:解答题
(本小题满分12分)下图是一几何体的直观图、主视图、俯视图、左视图.
(1)若 为
为 的中点,求证:
的中点,求证: 面
面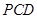 ;
;
(2)求A到面PEC的距离;

查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省高三第三次模拟考试理科数学 题型:解答题
下图是一几何体的直观图、正(主)视图、侧(左)视图、俯视图

(1)若 为
为 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)
下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]()
![]() 面
面![]() ;
;
(Ⅱ)证明![]() 面
面![]() ;
;
(Ⅲ)求面![]() 与面
与面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com