
【题目】Fibonacci数列又称黄金分割数列,因为当n趋向于无穷大时,其相邻两项中的前项与后项的比值越来越接近黄金分割数![]() .已知Fibonacci数列的递推关系式为
.已知Fibonacci数列的递推关系式为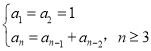 .
.
(1)证明:Fibonacci数列中任意相邻三项不可能成等比数列;
(2)Fibonacci数列{an}的偶数项依次构成一个新数列,记为{bn},证明:{bn+1-H2·bn}为等比数列.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用反证法,假设存在![]() ,
,![]() ,
,![]() 三项成等比数列,则
三项成等比数列,则![]() ,进而由已知关系证得
,进而由已知关系证得![]() 是无理数,这与其递推公式中反应的为有理数矛盾,得证;
是无理数,这与其递推公式中反应的为有理数矛盾,得证;
(2)由题表示![]() ,进而由已知
,进而由已知![]() 的递推关系表示出
的递推关系表示出![]() 的递推公式,再构造等比数列
的递推公式,再构造等比数列![]() ,进而由一一对应关系计算出对应参量,最后由等比数列定义得证.
,进而由一一对应关系计算出对应参量,最后由等比数列定义得证.
(1)证明:(反证法)假设存在![]() ,
,![]() ,
,![]() 三项成等比数列,则
三项成等比数列,则![]() ,
,
所以![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
由条件可知Fibonacci数列的所有项均大于0,所以![]() ,
,
又Fibonacci数列的所有项均为整数(由递推公式),所以![]() 应该为有理数,
应该为有理数,
这与![]() (无理数)矛盾(其相邻两项中的前项与后项的比值越来越接近黄金分割数,而不是恰好相等),
(无理数)矛盾(其相邻两项中的前项与后项的比值越来越接近黄金分割数,而不是恰好相等),
所以假设不成立,故原命题成立.
(2)证明:由条件得![]() ,
,![]() ,
,
所以![]() ,
,
即![]() ,
,
设![]() ,则
,则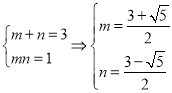 或
或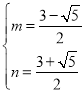
所以![]() 或
或![]()
所以![]() ,所以
,所以![]() 为等比数列,公比为
为等比数列,公比为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为4
的最小正周期为4![]() ,其图象关于直线
,其图象关于直线![]() 对称,给出下面四个结论:
对称,给出下面四个结论:
①函数![]() 在区间
在区间![]() 上先增后减;②将函数
上先增后减;②将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到的图象关于原点对称;③点
个单位后得到的图象关于原点对称;③点![]() 是函数
是函数![]() 图象的一个对称中心;④函数
图象的一个对称中心;④函数![]() 在
在![]() 上的最大值为1.其中正确的是( )
上的最大值为1.其中正确的是( )
A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.
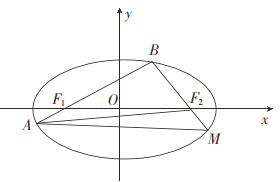
(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
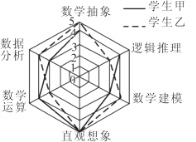
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.甲的六维能力指标值整体水平优于乙的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,
两点,![]() 的周长为8,直线
的周长为8,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆上两动点,线段
是椭圆上两动点,线段![]() 的中点为
的中点为![]() ,
,![]() 的斜率分别为
的斜率分别为![]() (
(![]() 为坐标原点),且
为坐标原点),且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:mx﹣y=1,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为_____,动直线l:mx﹣y=1被圆C:x2﹣2x+y2﹣8=0截得的最短弦长为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的长轴长与焦距之比为
的长轴长与焦距之比为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
(2)当线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距最小时,求直线
轴上的截距最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(﹣1,3),B(3,3)两点,且圆心C在直线x﹣y+1=0上.
(1)求圆C的方程;
(2)求经过圆上一点A(﹣1,3)的切线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com